[Generative] DDPM : Denoising Diffusion Probabilistic Models (NIPS'20)

• Paper : https://arxiv.org/abs/2006.11239
• Authors
  • Jonathan Ho et al, UC Berkeley, NIPS’20
• Main Idea
  • 기존 Diffusion 모델이 High Quality Sample을 Generation할 수 있다는 것을 보임.
  • ε-prediction reverse process parametrization 기법을 제안했는데, 기존의 Score-based 모델과 비슷한 면을 보임. 게다가 기존 Energe-based 와 Score-based 모델에 비해 estimate할 것이 많지 않은 장점을 가짐.
  • 대부분의 lossless codelength이 imperceptible한 이미지 표현에 사용된다는 것을 보였으며, lossy compression 기법을 통해 autoregressive 모델과의 유사성도 보임.
  • Tasks : Generative
  • Results : CIFAR-10

<구성>
0. Before Start ... 
   a. Bayes Rule
   b. VAE
   c. VAE의 ELBO
1. Problem 
   a. Diffusion
2. Approach 
   a. Forward Process
   b. Reverse Process
3. Results
   a. Setting
   b. Results

글효과 분류1 : 논문 내 참조 및 인용

글효과 분류2 : 폴더/파일

글효과 분류3 : 용어설명

글효과 분류4 : 글 내 참조

글효과 분류5 : 글 내 참조2

글효과 분류6 : 글 내 참조3

 

---

0. Before Start ... 

시작 하기 전에 알아 두어야할 부분이 있어 따로 챕터를 만들었습니다. Bayes Rule이 직접적으로 사용되지는 않지만, 기존에 딥러닝에서 사용되었던 확률분포관련된 이슈를 살펴보고, VAE에 대해 살펴보겠습니다.

---

a. Bayes Rule

 

확률 분포에 대한 Bayes Rule이란 확률론과 통계학에서 주로 쓰이며, 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리입니다. 보통 Probabilistic한 Bayesian Network에서 쓰이지만, Deterministic한 딥러닝에서는 어떤 의미를 가지는지 먼저 살펴보도록 하겠습니다.

 

$$ p(\theta|D)=\frac{p(D|\theta)p(\theta)}{p(D)}$$

$$ p(\theta|D)= p(\theta|x,y)=\frac{p(y|\theta,x)p(\theta)}{p(y|x)} $$

-----------------------------------------------------------------------------------------------------

<위 $\theta $,x,y로 된 식을 추정하는 과정>

Bayes Rule 등 확률 분포 간의 특징을 정리하면 몇가지가 있습니다.

• A. conditional probability : p(A|B) = p(A,B) / p(B)
  • p(A,B) = p(A|B)p(B)
• B. conditional probability : p(A,B|C) = p(A,B,C) / p(C)
• C. conditional probability : p(A,B|C) = p(A|B,C)p(B|C)
• D. when independent : p(A,B) = p(A)p(B)
• E. marginalization : 결합확률 분포를 전제로, 둘 중 하나의 확률 변수에 대한 확률 함수를 구하는 과정입니다.
  • marginal PMF(Probability Mass Function, 확률질량함수)
    $$P_X(x)=\sum_{y_i\in Y}^{}P_{X,Y}(x,y_i)$$
  • marginal PDF(Probability Density Function, 확률밀도함수)
    $$f_X(x)=\int_{y}^{}f_{X,Y}(x,y)dy $$

이 중 A와 C를 활용하면 아래와 같습니다. (용어 관련해서 아래 "용어"를 참조하세요)

$$p(\theta |y,x)=\frac{p(y|\theta ,x)p(\theta |x)}{p(y|x)}=\frac{p(y|\theta ,x)p(x,\theta)}{p(x,y)}$$

추가로 input x 와 model 파라미터인 $\theta $간의 독립이라는 특징을 활용하면 아래와 같이 정리할 수 있습니다.

$$\frac{p(y|\theta ,x)p(x,\theta)}{p(x,y)}=\frac{p(y|\theta ,x)p(x)p(\theta)}{p(y|x)p(x)}=\frac{p(y|\theta ,x)p(\theta)}{p(y|x)} $$

 

-----------------------------------------------------------------------------------------------------

• 용어
  
  • $\theta $ : Model Parameter, 현재의 증거
  • D : Data, 과거의 경험
    
    • x : input, y : output
  • 이전의 경험(D)과 현재의 증거($\theta $)를 토대로 어떤 사건의 확률을 추론
• 분포
  • p($\theta $|D) or p($\theta $|x,y) : Posterior Probability, 사후 확률, x,y가 이러한 모델은 뭘까? → 최종 Goal이지만 찾기 어렵다.
  • p(D|$\theta $) or p(y|$\theta $,x) : Likelihood, 조건부 확률(우도), 모델이 이러하고 x는 이런데 이때 y는 뭘까?, → 귀납적으로 반복(MLE)
  • p($\theta $) : Prior, 사전 확률, 방금 모델의 확률은?, → DL의 경우 모델의 확률을 알수가 없으므로, 모델을 업데이트 및 초기화하여 반영 후 무시합니다.
  • p(D) or p(y|x) : Evidence, 사전 확률, 관심없고, 비례식에 영향을 잘 주지 않는다, → 고정 혹은 무시

즉, 딥러닝에 있어서 우리의 목적은 p($\theta $|D), p($\theta $|x,y)를 찾는 일이다. 즉, "우리가 원하는 input/output인 x,y가 이런 상황인데 이것을 만족하는 모델 $\theta $는 무엇일까?"가 제일 궁금한 상황입니다. 하지만 딥러닝의 경우 최적의 모델일 확률인 p($\theta $)를 알기란 불가능하므로, Weight Initialization 혹은 Update를 반복하며 p(D|$\theta $) 값을 높여가는 것으로 진행합니다. 이를 MLE라고 합니다.

** MLE(Maximum Likelihood Estimation) : Likelihood P(D|$\theta $), 즉 Data D 가 모델 "$\theta $"를 따를 확률이 최대가 되도록 모델 "$\theta $"를 찾는 방법, 보통 Log Likelihood를 활용해 최소값을 찾는다

 

그렇다면 Bayesian Network는 어떨까? 위와 다른 부분만 표현하면 아래와 같습니다.

• 분포
  
  • p(D|$\theta $), p(y|$\theta $,x) : Likelihood, 조건부 확률(우도), 모델이 이러하고 x는 이런데 이때 y는 뭘까?, → 귀납적으로 반복(MAP)
  • p($\theta $): Prior, 사전 확률, 방금 모델의 확률은?, → Bayesian Netowkr 이므로 모델의 확률을 알 수가 있습니다. 귀납적으로 반복 MAP
    
    • ex) Gaussian Distribution이면 Model은 어느 정도 확률일 것이다 등등 계산 가능합니다.

위와 다른점은 그 모델일 확률 p($\theta $)를 Bayesian이기 때문에 알 수 있다는 것입니다. 따라서 이제는 원래의 goal 이었던 p($\theta $|D)를 정확하게 알아낼 수 있으므로, p($\theta $|D) 자체를 최대화하는 방향으로 학습을 진행합니다. 이를 MAP라고 합니다.

** MAP(Maximum A Posteriori) : MAP는 위와 다르게 Prior를 고려한 Prior x Likelihood가 최대가 되도록하는 것으로, 위에 보였던 MLE는 MAP의 특수한 경우라고 할 수 있습니다.

 

즉 위 내용을 정리해, MLE와 MAP의 차이를 그림으로 나타내면 아래와 같습니다.

MLE는 모델의 확률을 알 수 없다는 특징을 가진 MAP의 특수한 경우라고 볼 수 있으며, MAP는 모델의 확률을 알 수 있으므로 함께 고려해 찾을 수 있는 특징이 있습니다. 

[https://gaussian37.github.io/ml-concept-mlemap/]

---

b. VAE

 

VAE(Variational AutoEncoder)란 Generative Model의 한 종류입니다(Auto-Encoding Variational Bayes, arxiv'13). 아래 그림은 VAE를 도식화한 그림입니다.

[https://taeu.github.io/paper/deeplearning-paper-vae/]

모든 분포는 정규분포(Gaussian 분포)라고 가정되며, 먼저 가장 왼쪽의 Gaussian Encoder 부분에서는 input $x_i$에 대해 latent space인 $z_i$값의 평균과 분산을 얻어내는 과정입니다. 여기서 평균과 분산이 의미하는 바는, latent space의 "true 분포"를 의미합니다.
** Latent Space : 중간에 얻을 수 있는 feature vector가 있는 space를 의미하며, 주로 Latent Variable z 로 표현됩니다.

 

이후에 $z_i$값은 Decoder를 통해 아웃풋을 생성하게 됩니다. 당연히 Encoder를 통해 얻은 latent variable이, Decoder를 통해서 여러가지 output를 생성할 수 있도록 Sampling하는 과정이 포함되어야 합니다. 하지만 이 Sampling은 랜덤 프로세스(Random Process)이므로, 일반적인 네트워크처럼 back propagation할 수 없을 것 입니다.

 

따라서 Sampling을 아래 그림과 같이 따로해주고 난뒤에, Latent Variable인 평균과 분산에 반영을 하는 Reparametrization Trick을 활용합니다.

** Reparametrization Trick : 아래 그림과 같이 왼쪽의 "(정규분포에서 z를 바로 샘플링)"하는 것과, 오른쪽의 일반적인 (평균, 분산)을 구하고 "평균+(정규분포에서 epsilon을 샘플링)*분산"을 하는 것은 동일한 분포를 가지기 때문에, 어떤 필요에의한 trick이라고 생각하면 될 것 같습니다.

[https://arxiv.org/pdf/1906.02691.pdf]

-----------------------------------------------------------------------------------------------------

<Reparametrization Trick 증명>

Gaussian Noise가 아래와 같을 때 평균은 0, 분산은 1 입니다.

$$\epsilon \sim N(0,1)$$

 

이 때, z의 평균의 경우 아래와 같으며,

$$E[z]=E[\mu +\epsilon \sigma ]\\
=\mu +\sigma E[\epsilon ]\\
=\mu $$

 

z의 분산의 경우 아래와 같습니다.

$$Var[z]=E[z^2]-E[z]^2\\
=E[(\mu +\sigma \epsilon )^2]-\mu ^2\\
=E[(\sigma \epsilon )^2]\\
=\sigma ^2E[\epsilon ^2]\\
=\sigma ^2 $$

 

즉, z에서 샘플링을 하는 것은, noise ε에서 샘플링한 후에 분산을 곱하고 평균을 더하는 것과 같습니다.

-----------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------

** Auto Encoder(AE)와 Variational Auto Encoder(VAE)의 차이점 

AE와 VAE는 이름은 비슷하지만 근본적으로 목적이 다릅니다. 아래 그림에서 AE는 Gaussian Encoder를 알아내는 것이 목적이지만, VAE는 Bernoulli Decoder를 알아내는 것이 목적입니다.

[https://taeu.github.io/paper/deeplearning-paper-vae/]

• Auto Encoder(AE) : Input Data로부터 얻을 수 있는 feature를 가장 잘 표현할 수 있는 manifold를 얻어내는 것이 목적입니다.
  ** Manifold(다양체) : Data가 존재하는 공간이며, 다양한 차원으로 존재할 수 있습니다. 이렇게 Data가 존재하는 차원을 축소해 작은 차원으로 표현하면, 필요 매개변수가 적어지기 때문에 표현이 더 직접적이고 의미있는 경우가 많아 작은 차원으로 줄이려는 많은 시도가 있습니다.
  ex) 3차원의 Manifold → (Catesian 좌표계의 한 2차원 단면이 아닌) 공간상의 어떤 2차원으로 표현이 가능할 수도 있습니다.
• Variational Auto Encoder(VAE) : latent space z로부터 원하는 데이터 x를 얻는 것이 목적입니다. 따라서 p(x|z)를 얻어내는 것이 목적이며, 이 분포를 알아내면 z를 샘플링해서 x와 유사한 결과를 얻어낼 수 있습니다.

** Auto Regressive(AR) 란?

비슷한 용어이며 뒤에서 나오는 내용이 있어 이 또한 설명하고 지나가겠습니다. AR은 시계열 데이터를 처리하는데 사용되기도 하는 방법으로, 과거의 움직임에 기반해서 미래를 예측하는 방법입니다. 방법은 아래와 같으며, auto는 "자기 자신"을 의미하는데 여기서는 본인 과거의 값만을 사용하기 때문에 사용한 것으로 보입니다.

[Autoregressive의 예시]

-----------------------------------------------------------------------------------------------------

---

c. VAE의 ELBO

 

그럼 이제 위에서 살펴보았던 VAE의 모델을 학습하기 위해서는 어떤 loss 함수(최소화 목적) 혹은 objective function(최대화 혹은 최소화 목적)을 사용해야 할까요? 

** objective function의 경우 –log (negative log likelihood)로 표현해서 "최소화"를 하기도 하고, 그 자체로 최대화하기도 합니다.

 

앞서 살펴본 바와 같이 VAE의 목적은 decoder를 잘 학습하는 것이므로 결국 p_$\theta $()를 최대화하는 것이 목표라고 할 수 있습니다. 용어를 잠시 정리하고 가겠습니다.

• $q(z)$ : latent variable z의 분포 확률을 의미합니다.
• $q_\phi (z|x)$ : latent variable z 가 Encoder로부터 나올 확률입니다. Encoder는 Inference Model ϕ입니다
• $p(x)$ : input x의 분포 확률을 의미합니다.
• $p_\theta (x|z)$ : input x와 동일한 x가 Decoder로부터 나올 확률입니다. Decoder는 Infererence Model $\theta $입니다.

이제 우리의 목표는 input x의 분포가 잘 나올 확률 p(x)를 최대화 하는 것이 네트워크가 잘 학습하는 것이라고 할 수 있습니다. 최종 목적이 무엇인지 알았으므로, 먼저 p(x)에 대한 objective function을 풀어나간 순서를 보이겠습니다. 순서는 아래와 같습니다.

 

$$ \begin{matrix}
\textrm{log}p_{\theta }(x) = \textrm{log}p_{\theta }(x)\int q_{\phi }(z|x)dz\:\:\:(\because \int q_{\phi }(z|x)dz = 1)\\
= \textrm{log}\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)}\int q_{\phi }(z|x)dz\:\:\:(\because p_{\theta }(x)=\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)},\: bayes\:rule) \\
= \int \textrm{log}\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)}q_{\phi }(z|x)dz\:\:\:(\because Evidence\:Into\:Integral) \\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)}]\:\:\:(\because Monte\:Carlo\:Approximation) \\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)}\frac{q_{\phi }(z|x)}{q_{\phi }(z|x)}]\:\:\:(\because Multiple\:By\:1) \\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{q_{\phi }(z|x)}]+\mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{q_{\phi }(z|x)}{p_{\theta }(z|x)}]\:\:\:(\because Split\:the\:Expectation) \\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{q_{\phi }(z|x)}]+D_{KL}[q_{\phi}(z|x)||p_{\theta }(z|x)]\:\:\:(\because Definition\:of\:KL\:Divergence)\\
\geq  \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{q_{\phi }(z|x)}]\:\:\:(\because KL\:Divergence\:always\:\geq 0, ELBO)\\
\end{matrix}$$

 

위 식은 순서대로 따라가면 어렵지는 않을 것이라 예상합니다. 하지만 어떤 의미를 가지고 있을까요?

 

결과만 두고 얘기하자면 결국 우리가 원하는 결과를 얻기 위해서는 posterior인 $p_\theta (x|z)$를 알아내야하는데, posterior distribution의 경우 closed form이 아니므로 intractable합니다. (즉 무수히 많은 z에 대해 모든 계산하기 어렵습니다.) 따라서 우리가 알기 쉬운 분포인 Encoder의 $q_\phi (z|x)$를 도입해 , 이와의 분포차이를 알아냄으로써 문제를 해결하고자 하는 것입니다.

** Closed Form : 유한한 방법으로 표현한 수학적 표현입니다. 상수, 변수, 일반적인 연산, 함수 등으로 표현이 가능하면 Closed Form이며, 극한(특정 값과 무한히 작은 차이가 나도록), 적분(무한히 쪼개서 더한다), 미분(무한히 작은 범위에서의 범위를 본다) 등 무한의 개념이 들어가면 closed form이 아닌것입니다.
ex) 아래 예의 경우, 좌항은 closed form이 아니지만 우항은 closed form입니다.

$$\sum_{n=1}^{\infty }nx^n=\frac{x}{(1-x)^2}$$

** intractable : 고차원의 데이터를 다루거나 모델이 복잡한 경우, 적분 등의 문제를 해결하기 위한 시간이 Exponential 하게 증가하기 때문에 "난해하다"고 본다는 말입니다.

 

이렇게 구하기 어려운 분포를 다루기 쉬운 확률분포로 근사(approximate)하는 방법을 Variational Inference(VI)라고 합니다. 즉, 우리가 알고 있는 Variational Distribution이라 불리는 어떤 확률 분포 q_ϕ(z|x)를 가정하고, 우리가 원하는 $\theta $(모델)을 바꿔가며 이상적인 확률 분포에 Approximate하는 방법입니다.

-----------------------------------------------------------------------------------------------------

<Variational Inference(VI)>

변분추론(Variational Inference)란 위에서 언급한 바와 같이 closed form으로 표현되지 않거나 intractable한 경우, 다루기 어려운 분포를 최소화하기 위해서 이상적인 다른 분포를 가정하고, 해당 분포에 Approximate하기 위한 방법을 의미합니다.

• 방법1. Monte Carlo Sampling
  • “Sampling”이라고 이해하면 됩니다. 어떤 분포를 가정하고 그 분포에서 굉장히 여러번 샘플링을 해서 평균을 내면 전체에 대한 기댓값과 같아 질 것이다는 컨셉입니다. 즉, 랜덤 표본을 뽑아 함수의 값을 뽑아 확률적으로 계산하는 알고리즘입니다.
    $$\sum_{n=1}^{\infty}nx^n \Rightarrow \frac{x}{(1-x)^2}$$
• 방법2. Stochastic Variational Inference(SVI)
  • KLD를 줄이는 쪽으로 파라미터를 업데이트하는 방법으로 Stochatstic Gradient Descent를 활용합니다. 하지만 이 방식은 KLD가 미분가능해야 합니다.
  • 이 과정에서 Reparametriziation trick이 활용되기도 합니다.
• 방법3. Variation EM Algorithm
  • 물리학의 variational method에서 유래했습니다.
  • posterior p(z|x)를 알아내기 위해 q(z)의 파라미터와 p(x|z)를 동시에 알아내기 어려우므로, Expectation과 Maximization을 활용하는 방법입니다.
    ** Expectation : Monte Carlo방법 등을 활용해서 파라미터를 찾습니다.
    ** Maximization : ELBO를 찾아내고 이를 최대화하는 p(x|z)의 파라미터를 찾습니다.

-----------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------

<What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?(NIPS'17)>

예를 들어, 위 논문은 기존 딥러닝을 Bayesian Network형태로 가정해서 해당 모델의 Uncertainty(불확실성)을 알아보는 방법을 제안한 논문입니다. 해당 논문에서 관찰 결과에 따른 Aleatoric uncertainty와 모델 파라미터에 따른 Epistemic uncertainty을 소개합니다. 

• Aleatoric Uncertainty : 데이터 자체의 불확실성으로, 데이터를 많이 취득한다고 해도 줄일 수 없습니다. 이는 input에 무관한 homoscedastic과 input에 의존한 heteroscedastic으로 구분됩니다.
• Epistemic Uncertainty : 모델 파라미터의 불확실성으로, 데이터를 많이 취득하면 줄일 수 있습니다.

그 중 Epistemic Uncertainty를 구할 때 두가지 방법을 택합니다. 이 논문을 소개드리는 이유는, Variational Inference에서 알기 어려운 함수를 알아내는 방법으로 선택한 두가지 방법과 아래의 두가지 방법이 비슷하기 때문입니다.

• 방법1. Gaussian Distribution 등 Simple Distribution으로 가정하면 Bayesian Inference 방식을 사용해서 구해낼 수 있습니다. Bayesian Inference는 posterior distribution인 p($\theta $|D) 를 p($\theta $|D)≈q($\theta $) 와 같은 방법으로 근사화 하는 방법을 의미합니다. 
  • 아래 식과 같이 posterior 인 p($\theta $|x)를 알고 싶을 때, prior인 p($\theta $)에 대해 이미 알고 likelihood인 p(x|$\theta $)에 적절한 가정이 있다면 가능하다는 것입니다.
    $$p(\theta |x)=\frac{p(x|\theta )p(\theta)}{p(x)},\:\:p(x)= \int p(x|\theta )p(\theta )d\theta$$
• 방법2. Monte Carlo Dropout을 활용하면, 위 가정이 없어도 반복적으로 해서 알아 낼 수 있습니다. Monte Carlo Dropout이라 하면 반복적으로 추출해 결과를 추정해내는 방식입니다. 

-----------------------------------------------------------------------------------------------------

  

위 과정에서 모르는 단어가 나오기도 하는데 이에 대해 추가적으로 하나씩 설명하면 아래와 같습니다.

• Monte Carlo Approximation
  • 수식적으로는 어려울 수도 있지만, 단순히 말해 "엄청 많이 시도해보면, 정답을 알 수 있다"는 말입니다.
  • 어떤 데이터 $x_1, x_2, ... x_s$와 함수 f(x)가 있을 때, $[f(x_i)] (i=1,2,...s)$를 통해 결과 분포 f(X)를 근사할 수 있을 것 입니다. 이때 기대값을 구해내는 것이 Monte Carlo Approximation입니다.
  • $$\mathbb{E}[f(x)]=\int f(x)p(x)dx \approx \frac{1}{s}\sum_{S}^{i=1}f(x_{i})$$

• KL(Kullback-Leibler) Divergence
  • 두 확률 분포의 유사성을 측정하는데 사용하는 방법입니다.
  • 두 분포가 같으면 KLD는 0이며, 항상 0보다 크거나 같습니다.
  • $$KL(P(x)|Q(x)) = \int \textrm{log}\frac{P(x)}{Q(x)}P(x)dx$$

• ELBO(Evidence of Lower Bound), Variational Lower Bound(VLB), Proxy Loss
  • 위 식에서  “KLD가 0보다 크거나 같다”는 조건을 아래와 같이 활용해 찾아낸 Lower Bound를 ELBO라고 부릅니다.
  • 두가지 방식으로 이해할 수 있습니다.
    • 방식1. ELBO는 Lower Bound이므로, 이를 최대화하면 objective function이 최대화한다고 볼 수 있습니다.
    • 방식2. 어떤 Objective Function이 아래 그림과 같이 KLD인 $D_{KL}(q(z)||p(z|x))$과 ELBO의 합으로 표현될 때, ELBO를 증가시켜 KLD를 최소화한다고 생각하는 것입니다. 즉, p(x)는 학습데이터 x의 분포이므로 상수로 가정하고 ELBO를 최대화하면 KLD가 최소화 될 것이라고 보는 것입니다. 

[https://www.slideshare.net/NaverEngineering/ss-96581209]

 

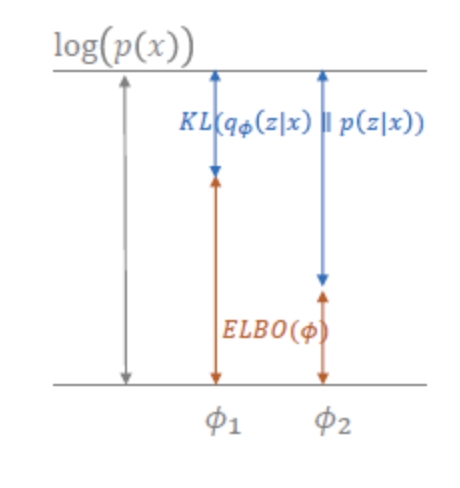
그렇다면 위 ELBO라는 식을 자세히 풀어보겠습니다.

$$ \begin{matrix}
\textrm{log}p_{\theta }(x)\geq  \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{q_{\phi }(z|x)}]\:\:\:(\because KL\:Divergence\:always\:\geq 0)\\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x|z)p_{\theta}(z)}{q_{\phi }(z|x)}]\:\:\:(\because Bayes\:Rule)  \\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}p_{\theta }(x|z)]+\mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta}(z)}{q_{\phi }(z|x)}]\:\:\:(\because Split\:the\:Expectation)\\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}p_{\theta }(x|z)]+D_{KL}(p_{\theta}(z)||q_{\phi }(z|x)])\:\:\:(\because Definition\:of\:KL\:Divergence) \\
\end{matrix}$$

 

위 최종적인 ELBO의 식 중, 앞에 것을 Reconstruction Error, 뒤에 것을 Regularization Error라고 부르기도 합니다.

• Reconstruction Error : 입력과 출력이 유사한 분포를 가지는지 측정하는 term 입니다. 즉, p(x|z)와 q(z|x) 사이의 negative cross entropy와 같기 때문에, encoder와 decoder가 auto-encoder처럼 reconstruction을 잘할 수 있게 만들어주는 error입니다.
• Regularization Error : posterior q(z|x)와 prior p(z) 간의 KL divergence와 같기 때문에, posterior와 prior가 최대한 비슷하게 만들어주는 error라고 할 수 있습니다. 이는 VAE가 reconstruction task만 잘하는 것을 방지한다고 합니다.

---

1. Problem 

기존에 아래와 같이 다양한 Deep Generative 모델들이 존재했습니다. 

• Autoregressive models
• Flows : [5][9][10][16][23][32][46]
• Variational Auto Encoders (VAEs) : [33] [37][47] 
• Generative adversarial networks (GANs)
• energy-based modeling(EBM) and score matching : [11][55]

본논문 DDPM이 나왔을 다시는 GAN성능 보다 아직 좋지 못했지만, 새로운 기법을 제안한 기여가 크며 이후에는 Generative Model Trilemma의 한축을 담당하게 됩니다.

[https://www.semanticscholar.org/reader/0d4154cbd76c4753ba3cb7a5b89ab29bab53384f]

-----------------------------------------------------------------------------------------------------

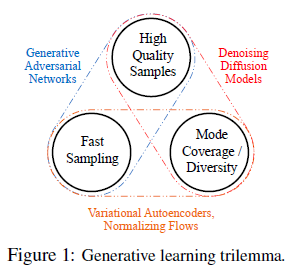
<Generative Trends>

이 논문을 읽기 전에는 이해하실 수 없겠지만, 혹시나 Background와 관련된 트렌드를 파악하시기 좋을 것 같아 stream을 적어 보았습니다.

• 개념을 소개한 논문
  • Deep Unsupervised Learning Using Nonequilibrium Thermodynamics (ICML’15)
• Diffusion 방식 발전
  • DDPM : Denoising Diffusion Probabilistic Models (NIPS’20)
  • DDIM : Denoising Diffusion Implicit Models (ICLR’21)
    • Random을 제거하면서 Deterministic하게 만들 수 있다
  • Improved DDPM (ICLR’21)
  • Diffusion Models Beat GANs on Image Synthesis (NIPS’21)
    • Classified Guidance 최초 제안
• NCSN(Noise Conditional Score Network) 혹은 SMLD(Score Matching with Langevin Dynamics) 방식
  • Generative Modeling By Estimating Gradients of the Data distribution (NIPS’19)
  • Score-Based Generative Modeling with Critically-Damped Langevin Diffusion (Nvidia)
    • score-based 를 velocity와 data로 분리해서 두번
• Diffusion방식과 NCSN방식을 통합한 개념
  • SDE로 diffusion process의 step간의 관계를 설명하다보니, Scored-based 방식과 Diffusion과 사실은 비슷한 개념이라는 것을 수학적으로 증명함.
    ** Stochastic Differential Equation(SDE) : stochatic한 부분이 포함된 미분방정식
    ** Ordinary Differential Equation(ODE) : 미분방정식
  • DDIM에서 처럼 Random을 제거하면서 Deterministic하게 만들 수 있다 : Probability Flow ODE
  • Score-based Generative Modeling Through Stochastic Differential Equations (ICLR’21)
• 이후에 소개된 내용
  • Conditional Diffusion 모델
  • 다양한 Down-stream Task와 관련된 논문 (fine-tuning 관련)
  • Sampling을 빠르게할 수 있는 방법
  • 다른 모델과 병합하는 방법

-----------------------------------------------------------------------------------------------------

---

a. Diffusion

 

기존에 Diffusion의 컨셉에 대해 제시한 논문(Deep unsupervised learning using non-equilibrium thermodynamics  (ICML’15)) 에서 diffusion에 대한 기본적인 컨셉에 대해 설명했기 때문에, DDPM에 앞서 Diffusion의 개념에 대해 간단히 소개하고자 합니다.

 

기존의 Diffusion의 컨셉은 forward process와 reverse process를 정의 하는 것으로 시작합니다.

 

[Forward와 Reverse Process]

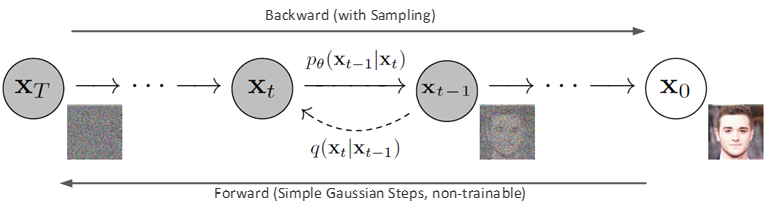
Forward process를 먼저 살펴보면, 실제 물리적으로 확산(diffusion)할 때, 어떤 분자의 '굉장히 작은' 다음 움직임은 gaussian 분포로 결정된다는 직관(intuition)에서 시작합니다. 이는 해당 논문의 제목에 언급된 비정형 열역학(Non-Equilibrium Thermodynamics)에 기초한 것이라고 볼 수 있습니다.

 

즉 이를 이미지에 적용해보면, 어떤 이미지가 있을 때 굉장히 작은 gaussian noise를 반복해서 더해주면 완전한 gaussian 형태의 분포로 변해갈 것이라는 컨셉에서 시작합니다.

 

또한 Reverse process는 이와 반대로, gaussian 형태의 분포에 gaussian noise를 반복해서 더해주면 이미지를 찾아 갈 수 있을 것이라는 가정으로 시작합니다.

 

이를 식으로 정의한 것은 아래와 같습니다. Forward process는 이미지에서 수 많은 gaussian noise를 더해주면 Isotropic gaussian noise(완전한 노이즈)가 될 것이므로 간단하겠지만, Reverse process는 어떤 noise를 더해주어야 할지 정하는 것이 쉽지 않을 것 같습니다.

 

Forward와 Reverse에 대해 정의한 것은 아래와 같습니다.

 

[Forward와 Backward(Reverse)의 정의]

 

---

 

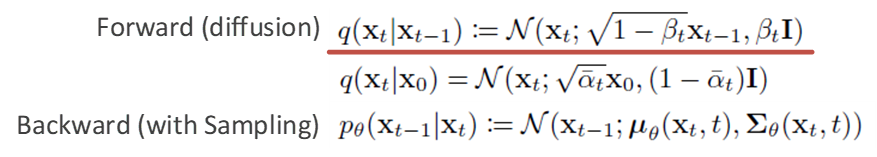
위 식에서 먼저 Forward Process를 살펴보면 이미지에 Gaussian Noise를 더해주는 과정인데, $\beta _t$가 굉장히 작을 때 t-1 step에서 t step으로 옮겨 갔을 때의 분포는 어떻게 되는지를 나타냈습니다.

 

이전 step의 feature에서 1에 가까운 값을 곱해 값을 조금 작게 만들어준 이후에, $\beta _t$분산을 더해줌으로써 약간의 noise를 더해주어 분포를 만들어 내는 방식이라고 할 수 있습니다.

-----------------------------------------------------------------------------------------------------

<Forward Process에 대한 추가설명>

위에서 본 바와 같이 Forward Process는 아래와 같이 정의 되었습니다.

$$q(x_t|x_{t-1})=N(x_t; \sqrt{1-\beta _t}x_{t-1}, \beta _tI)$$

우리는 확률분포의 특징을 아래와 같이 배운 적이 있습니다.

먼저 평균에 대해서, 상수c와 확률분포 X,Y에 대해 아래와 같은 성질을 같습니다.

$$\begin{matrix} 
E(c)=c \\ 
E(cX)=cE(X) \\ 
E(X+Y)=E(X)+E(Y) 
\end{matrix}$$
다음으로 분산에 대해서, 상수c와 확률분포 X,Y에 대해 아래와 같은 성질을 같습니다.
$$\begin{matrix} 
Var(x)\geq 0\\ 
Var(c)=0 \\ 
Var(cX)=c^2Var(x) \\ 
Var(X)=E(X^2)-E(X)^2 \\ 
Var(X+Y)=Var(X)+Var(Y) 
\end{matrix}$$

따라서 다시 원래 Forward Process를 살펴보면, $x_{t-1}$의 분산이 1이라고 가정했을 때, 분산이 1로 유지되는 것을 확인할 수 있습니다.

 

이런 특징 때문에 위와 같이 Forward Process를 디자인 한 것으로 보입니다.

-----------------------------------------------------------------------------------------------------

 

즉, VAE에서 설명드린 Reparametrization Trick까지 반영하면, 아래와 같이 Input 이미지 Pixel에 평균을 Element-wise Multiplication해준 이후, 분산과 Gaussian Noise에서 추출한 샘플을 Element-wise Multiplication해 둘이 더해주는 형태가 됩니다.

$$\begin{matrix}
x_t = \sqrt{\bar{\alpha }_t}x_0 + \sqrt{1-\bar{\alpha }_t} \epsilon \\ 
\epsilon \sim N(0,I)
\end{matrix}$$

 

여러개의 gaussian noise를 더하는 step들(0~t-1)은 연속된 process이므로, 이때 step별로 $\beta _t$를 정하는 것을 Noise Schedule이라고 하며, 이를 잘 정해주는 것이 중요합니다.

** 참고로 DDPM에서는 time stemp T는 1000, $\beta _0$는 0.0001, $\beta _1000$는 0.02로 schedule했습니다.

 

또한 기존의 다양한 $\beta _t$ 파라미터로 표현된 Noise들이 variance가 1로 유지되도록 모델링을 했으므로, 연속된 모든 step들을 합쳐 하나의 파라미터 $\bar{\alpha }$하나로 표현할 수 있다고 합니다. (중요!)

$$\begin{matrix} 
\alpha _t\approx 1-\beta _t \\
\bar{\alpha }_t\approx \prod_{s=1}^{t}\alpha _s 
\end{matrix}$$

** 타 논문에서는 이 특성을 "special property”혹은 “nice property”라고 부르기도 합니다

 

---

 

다음으로 Reverse Process에 대해 살펴보겠습니다. 앞서 말씀드린 것처럼 Isotropic gaussian noise(완전한 노이즈)에서부터 Noise를 제거해 점진적으로 이미지를 복원하는 과정입니다. 즉,  t step에서 t-1 step으로 옮겨 갔을 때의 분포는 어떻게 되는지를 알아내야 합니다.

 

하지만, reverse 과정에서 $p_\theta $로 얻어내 더해줄 Noise를 어떤 것으로 해야 할지 알기 어려운 상황입니다. 따라서 VAE에서 설명한 바와 같이 Objective Function을 최대화(혹은 최소화)하는 방법으로 진행합니다.

 

Objective Function을 VAE 에서 설명한 Variational Inference를 활용해 ELBO로 나타내면 아래와 같다고 합니다.

 

[ELBO를 구하는 과정]

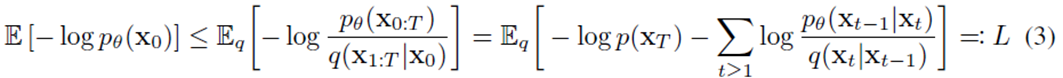
위 VAE와 다르게 ELBO가 부호 반대로 되는 이유는 –log 이기 때문이고, ELBO를 최대화하는 것이 Objective Function을 최소화하는 것과 같습니다.

 

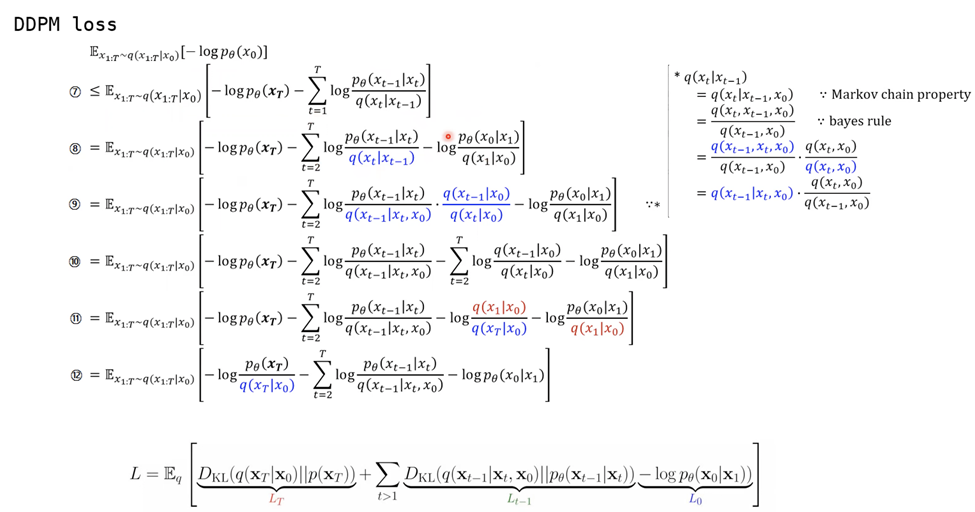
이런 ELBO값을 해당 논문에서 정리해나가면 아래와 같이 정리할 수 있다고 합니다. (얻어내는 과정을 아래 있는 더보기를 참조하세요)
** Markov Chain Rule이 활용됩니다.

[ELBO를 정리한 식]

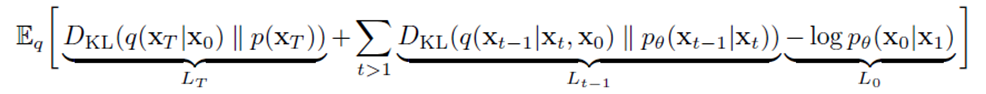
위 식을 조금 더 자세히 들여보겠습니다. 전체 적으로 E[]를 통해 평균하는 이유는 distribution의 평균값을 얻고 싶기 때문입니다. Loss 3개를 순서대로 아래와 같이 구분해 볼 수 있습니다.

• $L_T$ : Regularization Error, Prior Matching Term
  • 완전한 noise에 가장 가까운 term 입니다. 사전에 정의한 prior인 $p(x_T)$와 forward process를 통한 $q(x_T|x_0)$가 유사해지도록 KLD를 최소화하는 과정 
• $L_0$ : Reconstruction Error, Reconstruction Term
  • Noise를 추가해 완전한 이미지를 만드는 과정에 대한 term 입니다. T step의 개수가 클수록 가장 작은 비중이라는 말을 듣습니다.
• $L_{t-1}$ : Denoising Process Error, Denoising Term
  • 위 식중에 $L_{t-1}$이 가장 핵심 term이기도 하지만, 유일하게 tractable posterior distribution이기 때문에 아래와 같은 gaussian 분포들을 정의해 풀어나갈 필요가 있습니다.
    1. $q(x_{t-1}|x_t,x_0)$ : forward(diffusion), 실제 reverse process의 정답 분포, 알아낼 수 있습니다.
       ** 사실 $q(x_{t-1}|x_t)$는 알수가 없지만, $x_0$를 conditioning한 $q(x_{t-1}|x_t,x_0)$는 markov 정의가 깨지지 않으며 실제 값을 계산할 수 있습니다. 
       ** 즉, 원본 이미지 $x_0$와 step t 의 $x_t$가 있을 때, 평균과 분산으로 나타낼 수 있습니다. 
       $$\begin{matrix}
       q(x_{t-1}|x_t,x_0)=N(x_{t-1};\tilde{\mu _t}(x_t,x_0),\tilde{\beta _t}I)\\
       \tilde{\mu _t}(x_t,x_0)=\frac{\sqrt{\bar{\alpha }_{t-1}}\beta _t}{1-\bar{\alpha }_{t}}x_0 + \frac{\sqrt{\alpha _t}(1-\bar{\alpha }_{t-1})}{1-\bar{\alpha }_t}x_t = \frac{1}{\sqrt{\alpha _t}}(x_t - \frac{1-\alpha _t}{\sqrt{1-\bar{\alpha _t}}}\epsilon _t)\\
       \tilde{\beta _t}=\frac{1-\bar{\alpha }_{t-1}}{1-\bar{\alpha }_{t}}\beta _t
       \end{matrix}$$
       $$\begin{matrix} 
       \alpha _t\approx 1-\beta _t \\
       \bar{\alpha }_t\approx \prod_{s=1}^{t}\alpha _s 
       \end{matrix}$$
       
    2. $p_\theta (x_{t-1}|x_t)$ : reverse(generative), 알아내고 싶은 reverse process 모델의 확률

• • 결과적으로 우리가 알고 있는 forward $q()$를 활용해서 reverse 과정 $p_\theta ()$의 값을 알아내고자 한다는 것으로 이해할 수 있습니다. 
  • 둘다 Gaussian Distribution으로 가정했기 때문에, Rao-Blackwellized Fashion 으로 해결할 수 있습니다.

-----------------------------------------------------------------------------------------------------

 <VAE와 같이 DDPM의 loss를 추정하는 방법>

앞서 설명한 VAE에서 ELBO를 분석하여 표현한 것과 같이 DDPM에서 표현하는 방법을 자세히 살펴보면 아래와 같습니다.

 

먼저 DDPM의 ELBO를 구해내는 과정입니다. Markov chain의 특성을 활용해 풀어낸 것을 알 수 있습니다.

[https://www.youtube.com/watch?v=uFoGaIVHfoE &nbsp;]

 

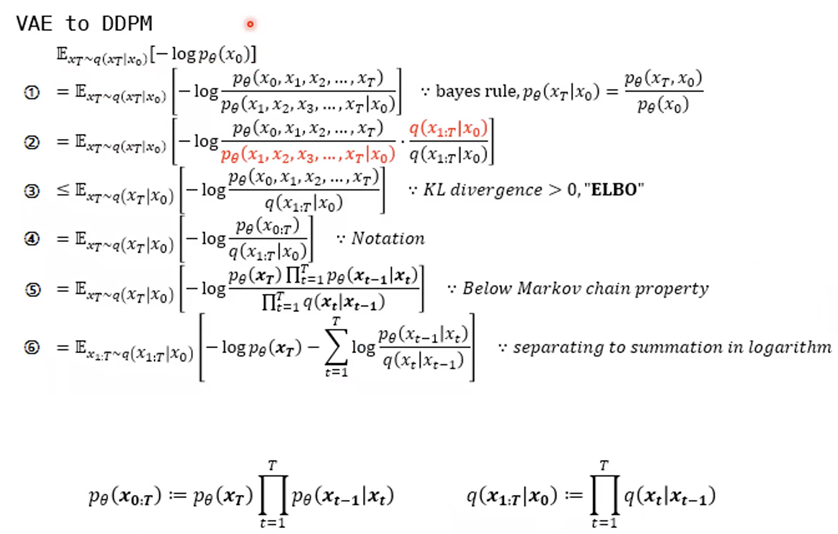
다음으로 ELBO를 자세히 분석해본 모습입니다. 역시나 Markov chain의 특성을 활용해 풀어낸 것을 알 수 있습니다.

[https://www.youtube.com/watch?v=uFoGaIVHfoE &nbsp;]

-----------------------------------------------------------------------------------------------------

-----------------------------------------------------------------------------------------------------

<Rao-Blackwellized Fashion 이란?>

간단하게, Gaussian distribution이기 때문에 VAE처럼 reparameterization trick으로 KL term을 학습하게 됩니다. 이를 위해 Closed Form Expression을 활용하며, High Variance Monte Carlo Estimates 대신 사용 가능합니다.

** Closed Form : 유한한 방법으로 표현한 수학적 표현, ∑𝑎 없이
 

자세히 표현하면 아래와 같습니다.

S는 충분통계량이고 U는 u에 대한 불편추정량 일때, 조건부 확률변수의 기대값 E[U|S]

• 1) E[E[U|S]]=u
• 2) Var(E[U|S]) < Var(U)

-----------------------------------------------------------------------------------------------------

 

결과적으로 위 objective fuction을 최대화하는 네트워크 $p_\theta $를 구하고, $p_\theta $를 통해 얻은 noise를 매 step마다 더해줌으로써 Reverse Process를 진행해주면 되겠습니다. 

 

그래서 우리가 알고 있는 q()를 통해 얻은 $p_\theta $는 평균과 분산으로 표현되어 있는데, 이들을 어떻게 표현될지는 아래에서 더 살펴보겠습니다.

---

2. Approach 

위와 같은 배경을 바탕으로 해당 논문에서는 다양한 접근을 통해 high quality sample을 생성할 수 있는 모델을 제안했습니다. 이는 위 배경에서 정의한 Forward Process와 Reverse Process(Backward)를 재정의함으로 진행하는데, 해당 내용을 자세히 살펴보도록 하겠습니다. 

 

설명하기에 앞서 Forward와 Reverse를 정의한 결과는 아래와 같습니다. 역시나 위에서 정의한 바와 같이, $p_\theta $가 reverse를 의미하고  q가 forward를 의미한다는 것을 알아두면 좋을 것 같습니다.

[Forward와 Backward(Reverse) Process]

 

---

a. Forward Process ($L_T$)

 

그럼 앞서 background로 살펴보았던 Loss식을 다시 한번 상기하면 아래와 같습니다. 

[ELBO를 정리한 식]

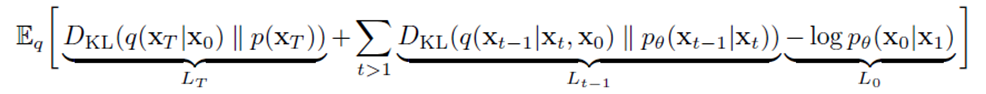
이번 챕터에서는 Forward process q()함수를 정의함으로써 ELBO에서의 $L_T$가 간단해질 예정입니다.

 

(복습) 먼저, 위에서 forward를 정의한 아래 식을 다시 상기해보겠습니다.

[Forward와 Backward(Reverse)의 정의]

 

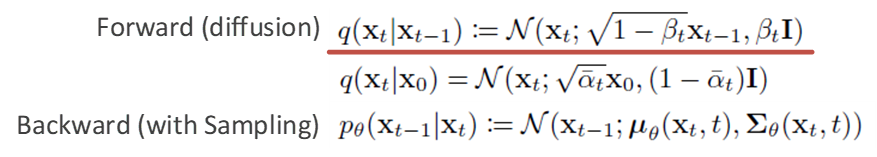
(복습) 기존의 임의의 t에 대한 forward process의 closed form은 아래와 같았던 것을 기억하실 겁니다.

$$q(x_t|x_0)=N(x_t; \sqrt{\bar{\alpha }_t}x_t, (1-\bar{\alpha }_t)I)$$

$$\begin{matrix} 
\alpha _t\approx 1-\beta _t \\ 
\bar{\alpha }_t\approx \prod_{s=1}^{t}\alpha _s 
\end{matrix}$$ 

본 논문에서는 q()를 정의하는데 사용 됐던 $\beta _t$를 non-learnable한 상수를 사용하겠다고 하고 있습니다. 이로인해 아래와 같은 ELBO식에서 q()는 학습이 되지 않는 parameter이므로, $L_T$는 항상 상수 인 것을 알 수 있습니다. 따라서 ELBO의 식이 아래와 같이 한층 간단해졌네요.

[L_T가 사라집니다]

---

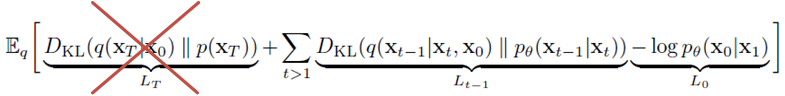
b. Reverse Process ($L_0$, $L_{t-1}$)

 

Reverse Process인 $p_\theta $() 를 정의해야합니다. $p_\theta $() 를 정의하는데 필요했던 분산과 평균을 어떻게 정했는지를 살펴볼 예정입니다.

 

위에서 남은 ELBO에 나오는 식들을 조금더 간단하게 표현해보다 보면, $p_\theta $() 가 어떻게 정의 되어야 하는 상황인지를 알게됩니다.

 

1. 더해질 Noise의 분산 대한 정의를 새로 정의합니다.

 

(복습) 다시, 위에서 reverse를 정의한 아래 식을 다시 상기해보겠습니다.

[Forward와 Backward(Reverse)의 정의]

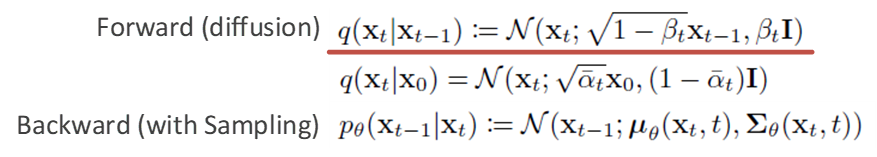
(복습) Step t에서 Step t-1로 가는 $p_\theta $의 기존의 정의는 아래와 같았습니다. 

$$p_\theta (x_{t-1}|x_t)=N(x_{t-1}; \mu _\theta (x_t,t), \sum_{\theta }^{}(x_t,t))$$

본 논문에서는 위 정의 중 분산을 아래와 같이 학습이 불가능한 time-dependent 상수를 활용하겠다고 하고 있습니다.

$$p_\theta (x_{t-1}|x_t)=N(x_{t-1}; \mu _\theta (x_t,t), \sigma _{t}^{2})$$

그래서, $\sigma ^2$ 즉, 분산은 뭘로 정의했다는 걸까요? 본 논문에서는 아래와 같이 실험적으로 정의했다고 하고 있습니다.

$$\sigma _{t}^{2}\approx \frac{1-\bar{\alpha }_{t-1}}{1-\bar{\alpha }_{t}}\beta _t\,\,\,or\,\,\,\beta _t$$

위 첫번째 분산은 $x_0$가 N(0,I)일 때의 최적화된 선택이고, 두번째 분산은 $x_0$가 하나의 point에 deterministic하게 모여 있을 때 최적화된 선택입니다. 본 논문에서는 전자를 선택했습니다.

 

---

 

2. 더해질 Noise의 평균에 대한 정의를 새로 정의합니다.

 

(복습) 위 1번의 분산 정의를 통해 아래와 같이 Reverse Process가 바뀌었습니다.

$$p_\theta (x_{t-1}|x_t)=N(x_{t-1}; \mu _\theta (x_t,t), \sigma _{t}^{2})$$

 

(복습) 또한 forward process q()는 평균과 분산으로 표현이 되며, 아래와 같이 정의가 가능했습니다. (1-a 참조)

$$\begin{matrix}
q(x_{t-1}|x_t,x_0)=N(x_{t-1};\tilde{\mu _t}(x_t,x_0),\tilde{\beta _t}I)\\
\tilde{\mu _t}(x_t,x_0)=\frac{\sqrt{\tilde{\alpha }_{t-1}}\beta _t}{1-\tilde{\alpha }_{t}}x_0 + \frac{\sqrt{\alpha _t}(1-\tilde{\alpha }_t-1)}{1-\tilde{\alpha }_t}x_t \\
\tilde{\beta _t}=\frac{1-\tilde{\alpha }_{t-1}}{1-\tilde{\alpha }_{t}}\beta _t
\end{matrix}$$

 

(복습) 현재 Loss는 $L_T$ term이 사라져 아래와 같이 간단해진 상황이고, 우리는 $L_{t-1}$ term을 살펴볼 계획입니다.

[L_T가 사라집니다]

 

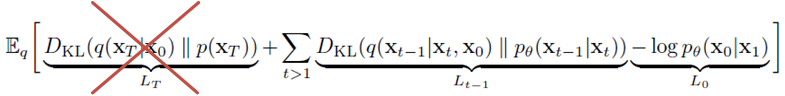
위 q()와 p() 정의를 활용해서 $L_{t-1}$ term을 풀어서 적어보면 아래와 같습니다.

$$\begin{matrix}
L_{t-1}=D_{KL}(q(x_{t-1}|x_t,x_0)|| p_\theta (x_{t-1}|x_t)) \\
=\mathbb{E}_q[\frac{1}{2\sigma _{t}^{2}}{\left\| \tilde{\mu _t}(x_t,x_0)- \mu _\theta (x_t,t)\right\|}^{2}]+C \\
=\mathbb{E}_{x_0,\epsilon }[\frac{1}{2\sigma _{t}^{2}}{\left\|\frac{1}{\sqrt{\alpha _t}}(x_t(x_0, \epsilon )- \frac{\beta _t}{\sqrt{1-\bar{\alpha }}_t}\epsilon ) - \mu _ \theta (x_t(x_0, \epsilon ),t)\right\|}^{2}]+C \\
= \mathbb{E}_{x_0,\epsilon }[\frac{\beta _t^2}{2\sigma _{t}^{2}\alpha _t(1-\bar{\alpha }_t)}{\left|\epsilon - \epsilon _\theta (\sqrt{\bar{\alpha }_t}x_0 + \sqrt{1-\bar{\alpha }_t}\epsilon, t)\right\|}^{2}]+C \\
= min||\epsilon - \epsilon _\theta (x_t,t)||^2+C
\end{matrix}$$

-----------------------------------------------------------------------------------------------------

<Gaussian Distribution Function>

가우시안 분포를 함수로 나타내면 아래와 같습니다.

$$g(x)=\frac{1}{\sqrt{2\pi \sigma ^2}}e^{-\frac{(x-\mu )^2}{2\sigma ^2}}$$

-----------------------------------------------------------------------------------------------------

 

위 Loss 식의 세번째 줄을 보면, 오른쪽의 reverse의 평균은 왼쪽의 형태와 같아지는 것이 목표라는 것을 알 수 있습니다. 즉 , $x_t$가 주어졌을 때 reverse process의 평균인 $\mu _\theta $가 되고 싶어하는 식을 약간의 parametrization을 통해 나타내면 아래와 같습니다.

$$\mu _\theta (x_t, t) = \frac{1}{\sqrt{\alpha _t}}(x_t -  \frac{\beta _t}{\sqrt{1-\bar{\alpha }}_t}\epsilon _\theta(x_t,t))$$

 

결과적으로 t step에서 t-1 step으로 가기 위한 $p_\theta (x_{t-1}|x_t)$는 위에서 정한 분산 $\sigma _t^2$와 포함해 아래와 같이 정의할 수 있습니다. (중요!)

$$x_{t-1}=\frac{1}{\sqrt{\alpha _t}}(x_t-\frac{\beta _t}{\sqrt{1-\bar{\alpha }_t}}\varepsilon _\theta (x_t,t))+\sigma _tz$$

** 이는 유한 시간 동안의 sampling chain을 찾아내는 아래와 같은 형태의 Langevin Dynamics 형태와 비슷하다고 합니다.

-----------------------------------------------------------------------------------------------------

<Langevin Dynamics 란?>

브라운 운동(Bownian motion, 아래그림 참조)을 stochastic process로 나타내는 미분방정식입니다. Langevin Dynamic을 이용해 sampling을 하는 것이 기존의 score-based generative model이라고 할 수 있습니다.

[https://hkilter.com/index.php?title=File:Brownian-motion.gif]

<Annealed Langevin Dynamic>

기존 Langevin Dynamic는 sampling을 하는 과정에서 Low data density를 반영하지 못했습니다.

** Low data-Density : Data의 밀도가 낮은 부분(데이터가 한쪽으로 몰려있을 때) 
따라서 각 step 을 T번 반복으로 실행하는 알고리즘을 활용하는 것이 Annealed Langevin Dynamic이고, 이를 활용하면 data distribution을 조금 더 반영해서 sampling할 수 있게 됩니다.

-----------------------------------------------------------------------------------------------------

참고로 뒤 실험에서 나오지만, 코드에서도 활용되기 때문에 언급하자면, $x_t$를 통해 바로 $x_0$를 아래와 같이 estimate할 수도 있습니다. (중요)

** 실제로 estimate는 가능하지만, 결과가 잘 나오지는 않습니다. 한번에 되지 않으니 여러번에 나눠 $x_0$를 찾아가는 과정의 noise를 미세하게 스케일링해 업데이트 한 것이라고 보면 될 것 같습니다.

$$\hat{x_0}=\frac{1}{\sqrt{\bar{\alpha _t}}}(x_t-\sqrt{1-\bar{\alpha _t}}\epsilon _\theta(x_t))$$

 

다시 Loss 로 돌아와 위 Loss식의 네번째 줄과 같이 정리했을 때, 다양한 Noise Schedule로 정해줄 수 있는 term들을 제외하면, 우리가 모르는 부분은 해당시점의 noise인 $\epsilon _\theta $에 대한 부분만 모르고 있고, 결국엔 위 Loss식 마지막 줄과 같이 해당 시점 t의 noise를 실제 noise와 L2 loss로 최소화하는 것이 목적이게 됩니다.

 

결론적으로, 우리의 Reverse 목적은

1. noise를 학습시키고
2. 해당시점 t의 noise를 알아내면,
3. 해당시점 t의 평균은 알수 있으므로,
4. 이를 활용해서 다음 t-1 step으로 갈 수 있게 된다는 것입니다.

[Forward Process와 Reverse Process]

---

 

3. Data Scaling ($L_0$)

 

마지막으로 $L_0$ term을 살펴볼 계획입니다. diffusion 모델을 활용했을 때, 최종 생성된 이미지를 만들어내는 과정에서의 loss입니다.

[L_T가 사라집니다]

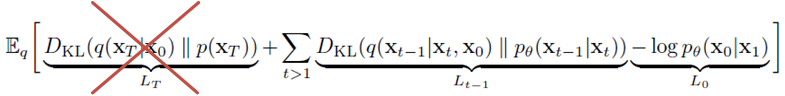
최종 생성된 이미지는 0~255의 값을 가질텐데, 이들을 [-1,1]로 linear하게 scaling이 가능하다고 가정했습니다. 따라서 Sampling의 마지막 단계인 $L_0=p_\theta (x_0|x_1)$는 discrete log likelihood를 가져야 하고, 이를 위해 마지막 단계는 아래와 같은 가우시안 분포를 활용한 독립적인 discrete decoder로 정했다고 합니다.

$$N(x_0;\mu _\theta (x_1,1),\sigma ^2_1I) $$

discrete decoder의 형태를 자세히 보면 아래와 같습니다.

$$\begin{matrix}
p_\theta (x_0|x_1)=\prod_{i=1}^{D}\int_{\delta _-(x^i_0)}^{\delta _+(x^i_0)}N(x;\mu _\theta ^i(x_1,1),\sigma ^2_1I)dx \\
\delta _+(x^i_0)=\left\{
\begin{matrix}
\infty ~if~x=1 \\
x+\frac{1}{255}~if~x<1
\end{matrix}\right.\\
\delta _-(x^i_0)=\left\{
\begin{matrix}
-\infty ~if~x=-1 \\
x-\frac{1}{255}~if~x>-1
\end{matrix}\right.
\end{matrix} $$

이런 선택은 우리가 만들 $L_0$를 포함한 loss가 discrete data의 lossless codelength를 보장한다고 하고 있습니다. 즉, 마지막 step(생성된 이미지로 가는 step)에서 추가적인 noise를 추가하거나 하는 것이 필요 없다는 것입니다.

** 기존에는 lossless codelength가 보장되지 않기 때문에 noise를 추가하거나, scaling operation을 통한 Jacobian 행렬변환이 필요했다고 하고 있습니다.

** lossless codelength와 뒤에 나올 Rate & Distortion에 대해 모르시면 아래 더보기를 참조하시는 것을 추천드립니다.

-----------------------------------------------------------------------------------------------------

<Lossy Compression>

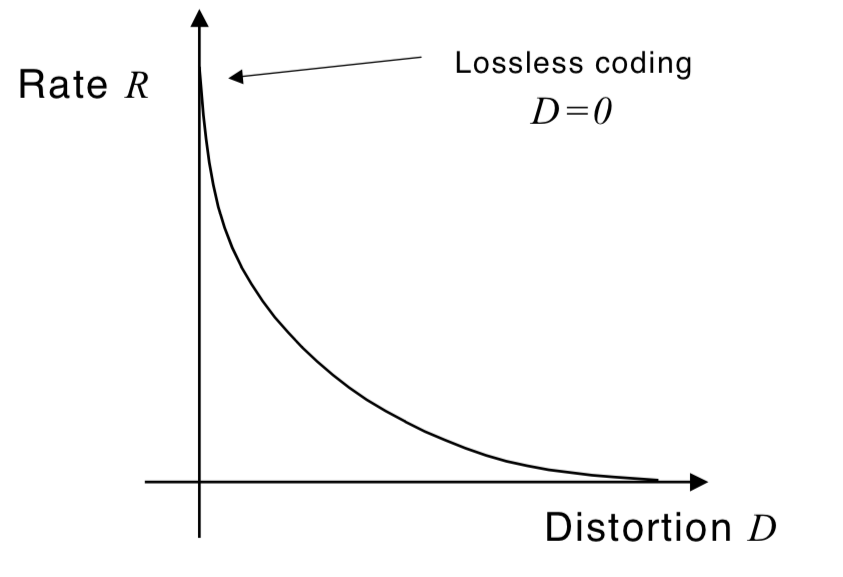
신호학 혹은 디지털 통신에서 주로 사용되는 것으로, signal compression과 관련된 용어입니다. 아래 그림과 같이, 어떠한 distortion(D)를 허용할 수록 code-rate(R)가 줄어들기 때문에 특정 수치 D*를 넘지 않으면서 R을 최소화하기 위한 연구를 rate-distortion 이론이라고도 불리기도 합니다.

 

quantization이 가장 실용적인 lossy compression의 예 입니다.

 

아래 보이는 것과 같이 distortion(D)가 0일 때, 혹은 rate(R)이 최대일 때를 lossless coding이라고 합니다.

[Rate-Distortion Plot]

 

<Code와 Symbol>

어떠한 정보가 있을 때 이를 신호로 표현하는 것을 Coding이라고 하고, 그 수단 bits들을 Code라고 합니다.

또한, 총 표현해야 할 Code의 종류가 M개 있을 때, 예를 들어 아래 식과 같은 k를 symbol이라고 합니다. 즉, 정보를 표현하기 위한 Code의 차원이 k bits symbol입니다. (다만, 항상 아래와 같지는 않을 수도 있습니다. 아래 Entropy관련된 설명을 참조하세요)

$$k=log(M)$$

 

<Rate와 Distortion>

Code Rate(R)은 symbol 당 필요한 bit의 수를 의미합니다. 즉, M개의 정보를 표현하기 위해서 k개의 bits 가 필요하다면, log(M)-k는 redundant일 것입니다. 따라서, 여기서의 Rate는 작을 수록 좋겠네요. (왜 k가 log(M)이 아닌지에 대해서는 아래 Entropy에 대한 설명을 참조하세요.)

$$R=\frac{k}{log(M)}$$

또한 Distortion(D)는 symbol을 u개 보냈을 때 몇개의 v가 들어오는지를 통해 계산할 수 있으며, 아래와 같은 조건을 만족합니다.즉, 생성모델에서는 복원된 정보와 기존정보의 차이를 의미하며 0에 가까울 수록 좋겠습니다.

$$\begin{matrix}
d(u,v)\geq 0 \\
d(u,v)=0~for~u=v 
\end{matrix}$$

 

<Entropy>
정보이론이라는 학문에서의 핵심은 "자주 일어나지 않는 사건은 자주 발생하는 사건보다 정보량이 많다"는 것입니다. 따라서 이에 따라 정보량을 표시하기 위해 정보 x에 대한 정보량은 아래와 같이 표현할 수 있습니다.
$$I(x)=-{log}_2p(x)$$
이렇게 자주 일어나지 않는 사건에 대한 정보량과, 해당 사건이 얼마나 자주 일어나는 지에 대한 정보를 합쳐 "정보량의 기댓값"을 표현한 것이 아래와 같은 Entropy입니다.
$$H(p)=\sum _ip_ilog(\frac{1}{p_i})=-\sum _ip_ilog(p_i)$$

예를 들어, 자주 일어나는 사건 A(90%)와 자주 일어나지 않는 사건 B(10%)가 있을 때, 이를 구분하는 1bit가 필요할 것입니다. 따라서, A사건에 대한 "정보량의 기댓값"은 0.9*(A'bits+1bits)일 것이고, B사건에 대한 "정보량의 기댓값"은 0.1*(B'bits+1bits)일 것입니다. 이때 B사건에 대부분의 bit를 활용하는 정보들이 포함될 것이기 때문에, 기대 되는 bit의 수가 줄어들 것이고, 이런식으로 위에서 이야기한 Rate를 줄일 수 있습니다.

이는 이후에 Cross Entropy의 개념과 합쳐 KL divergence를 표현하는데까지 이어 질 수 있습니다.
** KL-divergence : 최적의 결과인 Entropy와, 최적이 아닌 "일반인이 예상하는 확률"을 포함한 Cross-Entropy 의 차이를 의미합니다.
$$D_{KL}(P||Q)=-\sum _xp(x)logq(x) - (-\sum _xp(x)logp(x))$$

<Lossless Codelength> 
Entropy에 가까운 길이의 코드를 생성하는 데 사용되는 Compression Algorithm이 "distortion이 0에 가까우며(Lossless) rate가 적은", 좋은 lossy compressor가 완성되었다는 것을 의미합니다.

-----------------------------------------------------------------------------------------------------

 

---

 

4. Simplified Training Objective ($L_{t-1}$)

 

DDPM에서는 위 마지막으로 정의한 $L_{t-1}$에서의 Loss를 추가적으로 간단하게 할 수 있다고 합니다. 아래는 마지막으로 정의했던 $L_{t-1}$ term 입니다.

$$\mathbb{E}_{x_0,\epsilon }[\frac{\beta _t^2}{2\sigma _{t}^{2}\alpha _t(1-\bar{\alpha }_t)}{\left|\epsilon - \epsilon _\theta (\sqrt{\bar{\alpha }_t}x_0 + \sqrt{1-\bar{\alpha }_t}\epsilon, t)\right\|}^{2}]+C$$

아래와 같이 objective function 식의 weighting을 버리는 것이 더 유리하다는 것을 발견했다고 합니다.

 

[simplified objective without weighting]

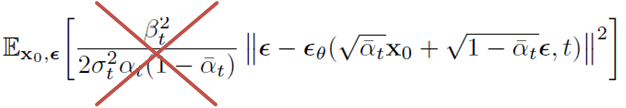
이유라고 하면, 원래 weighted variational bound를 활용하면 t가 증가할 수록 loss term을 down-weight하게되는데, 이를 없앰으로써 어려운 denoising task에 조금 더 focus할 수 있다고 하고 있습니다.

 

 

결과적으로는, $L_{t-1}$ term에서의 noise를 예측 하는 것이 목적이라는 것인데, 실제로 DDPM에서 차용한 model의 구조는 U-Net의 구조로, Input/Output의 차원이 일치하는 구조입니다. 아래 U-Net backbone에서는 아래와 같은 layer들을 활용했습니다.

• group normalization layer
• time embedding (sinusoidal)
• self-attention layer

[ https://www.youtube.com/watch?v=uFoGaIVHfoE &nbsp;]

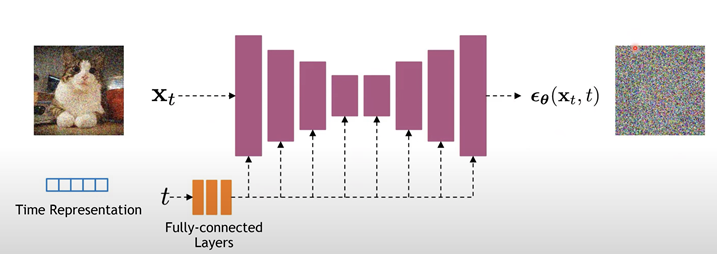
또한 학습 과정만을 살펴보면 아래 알고리즘과 같다고 합니다.

1. 이미지 $x_0$와 step t를 준비합니다.
2. Random Gaussian 에서 Noise  ε을 sampling 합니다. 이미지에 더해질 noise이자 target이 될것입니다.
3. UNet에 넣어줄 input을 기존 이미지 $x_0$와 noise를 통해 만들어줍니다.
4. UNet 구조를 통해 기존 이미지에 더해진 noise를 $\epsilon_\theta $라고 예측해냅니다.
5. $x_0$에서 $x_t$를 만드는데 추가된 ε에 대한 loss를 구해 업데이트 해줍니다.

--------------------------------------------------------------

<학습 과정에 대한 자세한 설명>

정확히 이해하기 위해 코드를 살펴보겠습니다.

 

diffusers 패키지에서 제공하는 학습 코드(https://github.com/huggingface/diffusers/blob/main/examples/unconditional_image_generation/train_unconditional.py)를 살펴보겠습니다.

 

0. input 이미지 $x_0$가 있습니다.

 

1~2. input 이미지와 같은 dim의 noise를 randn함수를 활용해 얻습니다. (Sampling)

noise = torch.randn(clean_images.shape, dtype=weight_dtype, device=clean_images.device)

 

 timestep은 랜덤하게 고릅니다. (Sampling)

# Sample a random timestep for each image
timesteps = torch.randint(
    0, noise_scheduler.config.num_train_timesteps, (bsz,), device=clean_images.device
).long()

 

3. 위에서 얻은 noise와 원래 image를 더합니다. 이때 t step의 alpha를 활용합니다.

$$\sqrt{\alpha _t}\cdot x_t+ \sqrt{(1-\alpha _t)}\cdot \epsilon _t$$

noisy_images = noise_scheduler.add_noise(clean_images, noise, timesteps)

 

4. 위에서 얻은 noisy_image를 input으로 하는 UNet의 결과를 얻어 냅니다. 

** UNet의 결과가 이미지 자체인 sample일 수도 있고, noise인 epsilon일 수도 있지만 epsilon이라고 가정하겠습니다.

model_output = model(noisy_images, timesteps).sample

 

5. 4의 결과와 1번에서 sampling한 noise간의 loss를 구합니다. 즉, 이미지에 더해진 noise를 찾는 역할을 합니다.

loss = F.mse_loss(model_output.float(), noise.float())  # this could have different weights!

--------------------------------------------------------------

 

이번엔 sampling과정을 살펴보면 아래와 같습니다.

1. 현재 상태의 Noisy한 이미지 $x_{t}$를 활용해 해당시점에 껴있을 Noise $\epsilon _\theta $를 UNet구조를 통해 예측해냅니다.
2. 예측된 noise를 활용해 이전 step의 noisy image를 구해줍니다.
3. 1~T번을 반복합니다.

--------------------------------------------------------------

<Sampling 과정에 대한 자세한 설명>

정확히 이해하기 위해 코드를 살펴보겠습니다.

 

diffusers 패키지에서 보통 기존의 모델을 활용해 inference하는 기본적인 코드는 아래와 같습니다.

from diffusers import DDPMPipeline

ddpm = DDPMPipeline.from_pretrained("google/ddpm-cat-256", use_safetensors=True).to("cuda")
image = ddpm(num_inference_steps=25).images[0]

 

따라서 메인 클래스라고 볼 수 있는 DDPMPipeline클래스의 __call__()함수(https://github.com/huggingface/diffusers/blob/main/src/diffusers/pipelines/ddpm/pipeline_ddpm.py)를 살펴보겠습니다.

0. timestep t의 순서로 진행되기 때문에 timestep t를 step0부터 순서대로 진행합니다.

 

여기에 추가로 초기 initial noise $x_T$를 구해냅니다. (Sampling)

** 정해진 이미지 여러장을 생성하고 싶다면 initial noise 여러개를 준비합니다.

** initial noise의 중요성에 대해 언급하고 싶어 아래 추가로 더보기를 만들었습니다.

image = randn_tensor(image_shape, generator=generator, device=self.device)

 

1. UNet을 통해 model_output, $\epsilon _\theta $를 얻어냅니다.

** UNet의 결과가 이미지 자체인 sample일 수도 있고, noise인 epsilon일 수도 있지만 epsilon이라고 가정하겠습니다.

model_output = self.unet(image, t).sample

 

*********************************************************************
2. 위에서 얻은 model_output, timestep, sample(image)을 통해 다음 step의 이미지를 예측해낼 계획입니다. 해당 과정은 이제 DDPMScheduler 클래스의 step함수(https://github.com/huggingface/diffusers/blob/35db2fdea91dad8842d6d083d68e396c81b9e771/src/diffusers/schedulers/scheduling_ddpm.py)에서 진행됩니다.

image = self.scheduler.step(model_output, t, image, generator=generator).prev_sample

*********************************************************************

 

2-1. $\bar{\alpha }_t$, $\bar{\alpha }_{t-1}$, $\bar{\beta }_t$, $\bar{\beta }_{t-1}$를 미리 구합니다. 

** bar표시는 앞서 정의한 바와 같이 해당 step까지의 hyperparameter를 곱한 값을 의미합니다.

# 1. compute alphas, betas
alpha_prod_t = self.alphas_cumprod[t]
alpha_prod_t_prev = self.alphas_cumprod[prev_t] if prev_t >= 0 else self.one
beta_prod_t = 1 - alpha_prod_t
beta_prod_t_prev = 1 - alpha_prod_t_prev
current_alpha_t = alpha_prod_t / alpha_prod_t_prev
current_beta_t = 1 - current_alpha_t

2-2. sample $x_t$,  model_output $\epsilon _\theta (x_t)$을 아래 식에 의해 더해 예측된 $x_0$를 구해냅니다.  이를pred_original_sample이라 하겠습니다.

$$\hat{x_0} = \frac{1}{\sqrt{\bar{\alpha}_t}}(x_t-\sqrt{1-\bar{\alpha}_t}\epsilon _\theta(x_t))$$

# 2. compute predicted original sample from predicted noise also called
# "predicted x_0" of formula (15) from https://arxiv.org/pdf/2006.11239.pdf
pred_original_sample = (sample - beta_prod_t ** (0.5) * model_output) / alpha_prod_t ** (0.5)

2-3. 앞서 구한 $\hat{x_0}$, pred_original_sample과 sample $x_t$을 아래 식에 의해 더해 평균 $\tilde{\mu _t}$을 구해냅니다.

$$\tilde{\mu _t}(x_t,x_0)=\frac{\sqrt{\bar{\alpha }_{t-1}}\beta _t}{1-\bar{\alpha }_{t}}x_0 + \frac{\sqrt{\alpha _t}(1-\bar{\alpha }_{t-1})}{1-\bar{\alpha }_t}x_t = \frac{1}{\sqrt{\alpha _t}}(x_t - \frac{1-\alpha _t}{\sqrt{1-\bar{\alpha _t}}}\epsilon _t)$$

# 5. Compute predicted previous sample µ_t
pred_prev_sample = pred_original_sample_coeff * pred_original_sample + current_sample_coeff * sample

 

2-4. 아래식과 같은 variance $\tilde{\beta _t}$를 섞어 결과인 pred_prev_sample $x_{t-1}$을 얻습니다. (Sampling)

$$\tilde{\beta _t}=\frac{1-\bar{\alpha }_{t-1}}{1-\bar{\alpha }_{t}}\beta _t$$

# 6. Add noise
# For t > 0, compute predicted variance βt (see formula (6) and (7) from https://arxiv.org/pdf/2006.11239.pdf)
# and sample from it to get previous sample
variance_noise = randn_tensor(
                model_output.shape, generator=generator, device=device, dtype=model_output.dtype
            )
variance = (self._get_variance(t, predicted_variance=predicted_variance) ** 0.5) * variance_noise

pred_prev_sample = pred_prev_sample + variance

 

 결과적으로는 얻은 pred_prev_sample $x_{t-1}$은 아래 식과 같을 것입니다.

$$x_{t-1}=\frac{1}{\sqrt{\alpha _t}}(x_t-\frac{\beta _t}{\sqrt{1-\bar{\alpha }_t}}\varepsilon _\theta (x_t,t))+\sigma _tz$$

 

--------------------------------------------------------------

--------------------------------------------------------------

<Initial Noise의 중요성>

 

initial noise에 대해 여러개의 이미지를 위한 준비작업으로 생각할 수도 있지만, 필자의 의견을 좀 담아보고자합니다.

 

Visual Style Prompting with Swapping Self-Attention(arxiv'24)라는 논문은  따르면 같은 weight를 가진 UNet을 준비합니다. 두 네트워크는 각각 아래와 같은 기능을 합니다.

• 기존의 Style을 그대로 생성하는 Style Reconstruction
• 새로운 컨텐츠를 생성하는 Content Generation

이 때, Style Reconstruction을 하는 네트워크의 initial noise는 해당 reference image에 의해 생성되겠지만, Content Generation을 하는 네트워크의 initial noise는 랜덤 noise를 활용합니다.

** 물론 DDPM의 sampling은 stochastic하므로, 이 논문에서는 DDIM이라는 deterministic한 sampling을 사용했습니다. DDPM은 initial noise가 같아도 다양한 생성이 stochastic하게 가능하지만, DDIM은 같은 initial noise가 같으면 같은 이미지를 만들어냅니다.

 

이때 Inference time에, style에 대한 학습없이, Style Reconstruction의 중간 activation들을 Swapping Self-Attention이라는 기법을 활용해 Content Generation하는 네트워크에 사용하고, Style Reconstruction의 style과 비슷하게 Content를 생성해냅니다.

[다른 Initial Noise의 intermediate activation을 활용한 예 ]

 

이 결과물을 보아, 필자는 물론 중간의 어떤 layer의 feature를 활용하는지도 중요하겠지만 생성하는 결과물의 style에 있어서 initial noise가 중요한 역할을 할 수도 있겠다는 생각을 했습니다. 

--------------------------------------------------------------

 

[학습과정과 Sampling 과정]

---

3. Results 

DDPM에서 보여준 결과들을 정량 및 정성적으로 살펴보겠습니다.

---

a. Setting

먼저 위에서 정의한 내용에 대해 설명하면 아래와 같습니다.

• T : 1000
• $\beta _1$ = $10^{-4}$ ~ $\beta _T$=0.02 (linear noise schedule)
  • 상수로 정함으로써 reverse와 forward가 거의 같은 functional form을 가지게 할 수 있습니다.
  • $x_T$의 SNR(Signal-To-Noise)을 최소한으로 유지할 수 있습니다. 완전한 Noise와의 KLD가 $10^{-5}bits/dim$이었다고 합니다.
• Network : U-Net backbone
  • unmasked PixelCNN++를 활용 (PixelCNN++:Improving the PixelCNN with discretized logistic mixture likelihood and other modifications, ICLR'17)
  • 사용한 layer들은 앞서 언급한 layer들과 같습니다.
• Dataset
  • Quantitative(정량적) & Qualitative(정성적) : CIFAR-10
  • Qualitative(정성적) : CelebA-HQ, LSUN

 

---

b. Results

 

• Sample Quality

먼저 sample의 quality를 정량적으로 살펴보기 위해 Inception score와 FID score를 나타낸 표는 아래와 같습니다. FID가 training set에서는 3.17, test set에서는 5.24인데 대부분의 다른 model들 보다 좋은 성능이라고 얘기하고 있으며, 심지어 conditional generative model들 보다도 좋다고 하고 있습니다.

[CIFAR-10 results]

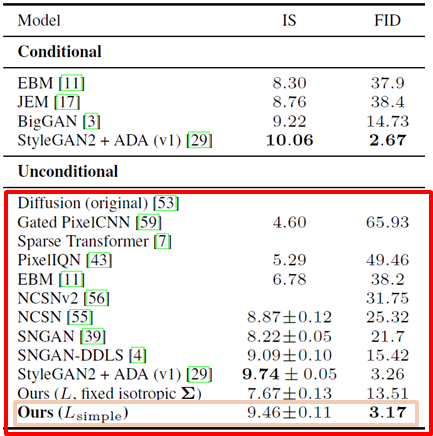
** 평가 Metric에 대해 모르시는 분들은 아래 더보기를 참조하세요

-----------------------------------------------------------------------------------------------------

< Evalutation Metric >

보통 Generative Model을 평가할 때 두가지 관점에서 평가합니다. 먼저, Quality는 실제 이미지와 유사한 이미지가 생성되는가를 보며, 다음으로 Diversity는 여러 noise vector에 걸쳐 다양한 이미지가 생성되는가를 봅니다.

• IS (Inception Score) : 높을 수록 good
  
  • ImageNet pretrained inception-v3를 이용하여 GAN을 측정
  • P(y|x) : Fidelity(질),  Generated x에 대해 y 클래스라고 sharp하게 classification하면(entropy 낮음) 고화질
  • P(y) :  Diversity(다양성), 클래스 y가 다양하게 나오면 (entropy 높음) 다양하다
  • $$IS = exp(\mathbb{E}_{x\sim p_{data}}D_{KL}(P(y|x)||P(y)))$$
• FID(Fréchet Inception Distance) :낮을 수록 good
  
  • ImageNet pretrained inception-v3를 이용하여 GAN을 측정
  • feature extractor : 실제 이미지와 생성된 이미지 사이의 activation map을 각각 추출
  • 실제 이미지의 확률 분포와와 생성된 이미지의 확률 분포 사이의 Wassertein-2 distance
  • $$FID=d^2=||\mu _1-\mu _2||^2_2-Tr(\sum _1+\sum _2-2 \sum _1 \sum _2)$$
• LPIPS (Learned Perceptual Image Patch Similarity) : 낮을 수록 good
  
  • 기존의 IS나 FID와는 다르게 유사도를 사람의 인식에 기반하여 측정
  • ImageNet pretrained AlexNet, VGG, SqueezeNet에 두 이미지를 넣어 activation map을 각각 추출
  • 두 이미지 사이의 Euclidean distance
  • $$LPIPS=\sum _l\frac{1}{H_lW_l}\sum _{h,w}||w^l\odot (\hat{y}^l_{hw}-\hat{y}^l_{0hw})||^2_2$$

-----------------------------------------------------------------------------------------------------

또한 정성적으로 살펴보았을 때도 아래와 같이, 좋은 결과를 냈다고 하고 있습니다.

[Celeb-A-HQ 256x256(왼쪽)과 CIFAR10(오른쪽)]

[LSUN]

 

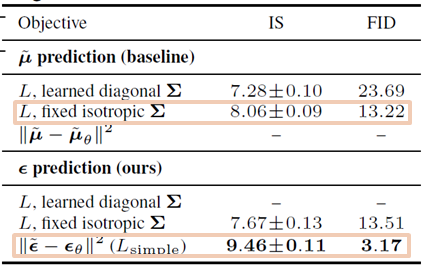
• Training Objective Ablation

본 논문에서 진행한 reverse process의 parametrization의 효과를 보기 위한 ablation study결과는 아래와 같으며, 비어져 있는 부분은 학습하기에 stable하지 않기 때문에 누락했다고 되어있습니다.

- learned diagonal : 분산이 학습이 가능할 때의 결과

- fixed isotropic : 분산을 상수로 고정했을 때(1-b 참조)의 결과

- noise L2 : 분산을 상수로 고정했으며, noise의 L2 loss와 simplified objective(1-b 참조)를 활용한 경우의 결과

 

결과적으로 평균 µ보다는 noise를 predict했을 때가 더 안정적이며, variational bound의 경우 fixed variance와 simplified objective를 활용했을 때 가장 성능이 좋다고 합니다.

[CIFAR-10 Results]

 

• Progressive Coding - Codelength (NLL table)

위에서 보았던 표를 아래와 같이 다시 살펴보면, codelength에 대한 결과를 다시 볼 수 있습니다. 

[CIFAR-10 results : codelength를 보기 위한 NLL table]

 

먼저, train과 test의 codelength 차이가 0.03bits/dim 인 것으로 보아 overfitting되지 않았다는 것을 알 수 있습니다.

 

또한 앞서 마지막 sampling에서 제안한 lossless codelength기법이 (2-b 참조) 많은 estimate들을 필요로 하는 기존의 EBM(Energe-based Model)이나 Score Matching 기법 보다 더 낫다고 하고 있습니다.

 

그리고 본 논문에서 제안하는 모델의 sample들이 높은 퀄리티를 가진 것으로 보아 모델이 inductive bias 를 가지고 있다고 하고 있습니다.

** inductive bias는 좋은 lossy compressor를 만들어냅니다. (distortion을 최소화하며 rate를 최소화)

 

마지막으로 NLL 테이블을 보면, DDPM의 NLL(Negative Log Likelihoods)은 3.75bits/dim인데, "$L_0$를 distortion" "$L_1$~$L_T$를 rate"라고 했을 때, distortion이 1.97bits/dim 이며 rate가 1.78bits/dim이었다고 합니다. 본 논문에서 제안한 lossless codelength의 절반 이상이 거의 찾을 수 없는 "distortion"인 것을 확인 할 수 있습니다.

 

• Progressive Coding -Progressive Lossy Compression

위의 내용을 조금 더 살펴보기 위해 제안한 모델의 rate-distortion 형태에 대해 살펴보기 위해, 본 논문에서 제안한 알고리즘과 똑같은 progressive lossy code를 보인다고 하고 있습니다. 이는 기존에 보였던 아래 ELBO식을 활용해 만들어냈습니다.

[ELBO를 정리한 식]

 

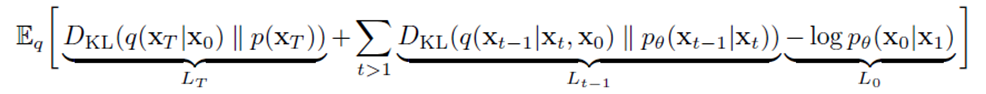
해당 논문에서 제안한 progressive lossy code에 대해 살펴보겠습니다.

 

먼저, Sending을 살펴보면 p(x) 분포를 알고 있기 때문에 아래 KL Divergence 식을 통해 q(x)를 만들어 sample x를 보내는 것이 목표입니다. 즉, "예상되는 codelength"(평균)를 활용해 q(x)를 만들고 sample을 보내는 것입니다.

$$approximately~D_{KL}(q(x)||p(x))~bits~on~average$$

1. $p(x_T)$를 활용해 $q(x_T|x_0)$를 구하고 $x_T$를 만들어 낸 후에 $x_T$를 보냅니다.
2. $p_\theta (x_t|x_{t+1})$을 활용해 $q(x_t|x_{t+1},x_0)$를 구하고 $x_{T-1}$ 부터 $x_1$까지를 만들어 보냅니다.
3. $p_\theta (x_0|x_1)$을 활용해 $x_0$를 만들어 보냅니다.

 

다음으로, Receiving을 살펴보면 p(x)분포를 알고 있기 때문에, Sender로부터 받은 sample x를 활용해 아래와 같이 estimate했습니다.
$$x_0\approx \hat{x_0}=(x_t-\sqrt{1-\bar{\alpha _t}}\epsilon _\theta(x_t))/\sqrt{\bar{\alpha _t}}$$

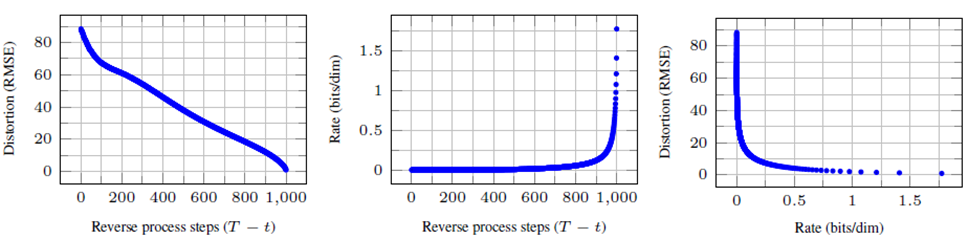
그다음 아래와 같은 RMSE(Root Mean Squared Error)식을 통해 distortion을 측정합니다.

$$\sqrt{||x_0-\hat{x_0}||^2/D}$$

그 다음 step t 까지의 누적된 bits수를 활용해 rate를 측정합니다.

 

아래는 그 순서입니다. (?? 확인중입니다. TODO)

1. $x_T$를 받습니다. (p(x_T)를 활용)
2. $x_{T-1}$ 부터 $x_1$까지를 받습니다. ($p_\theta (x_t|x_{t+1})$을 활용)
3. $x_0$를 받습니다 ($p_\theta (x_0|x_1)$을 활용)

[progressive lossy code]

아래 마지막 그림은 위 방법으로 알아낸 rate-distortion plot을 나타냅니다. 본 논문에서는 distortion이 굉장히 steeply하게 감소되는 것을 보아, 대부분의 bits들이 보이지 않는 distortion에 속해있다는 것을 알 수 있다고 합니다. 즉, distortion이 굉장히 작으면서도 rate가 충분히 작은 lossless codelength를 만족한다는 것을 의미합니다.

[rate-distortion plot]

 

• Progressive Generation

이번엔 reverse process에서 t step별로 어떤 feature를 담당하는 noise가 추가되는 지를 살펴보는 것입니다.

- t가 클수록 : large scale feature(coarse contents)이 나타나기 시작합니다.

- t가 작을수록 : fine detail(low-level details)이 나타나기 시작합니다.

 

 

• Connection to Autoregressive Decoding

이번엔 기존에 우리가 살펴보면 ELBO식을 아래와 같이 다시 적어보았습니다.

[Autoregressive Decoding과의 유사성 분석]

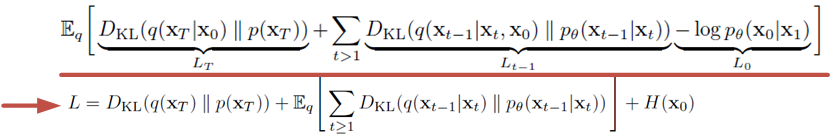
기존에 우리가 정했던 step T를 data의 추가적인 dimension이라고 가정하고 식을 분석해보았습니다.

• forward process인 $q(x_t|x_0)$는 앞 t개의 $q(x_t|x_{t-1})$ coordinate를 mask한 다음 $x_0$에 대한 확률을 를 찾아내는 형태일 것입니다.
• $p(x_T)$는 blank image에 대한 확률을 찾아내는 형태일 것입니다.
• $p_\theta (x_{t-1}|x_t)$는 전체적인 conditional distribution을 활용하는 형태일 것입니다.

 

위와 같이 만든다면 아래와 같이 $x_T$에 대한 forward와 reverse의 KL Diveregence인 첫번째 항은 0일 것입니다.

$$D_{KL}(q(x_T)||p(x_T))=0$$

또한 두번째 항인 아래 식은 t+1...T번째 coordinate를 활용해 t번째 coordinate를 예측하는 형태일 것입니다. 이런 형태가 autoregressive model과 같은 형태라고 하고 있습니다.

$$D_{KL}(q(x_{t-1}|x_t)||p_\theta (x_{t-1}|x_t))$$

 

위에서 정의한 아래 식의 forward를 다시 살펴보겠습니다. 

[Forward와 Backward(Reverse)의 정의]

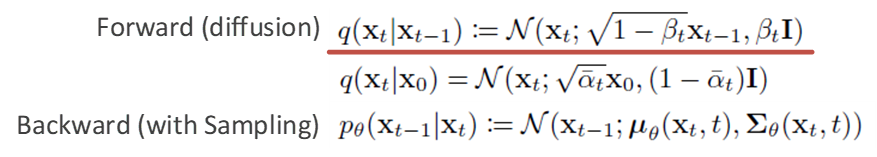
위에서의 t는 reordering해서 표현할 수 없으므로,  autoregressive model의 generalized bit ordering과 비슷하다고 볼 수 있습니다.

 

하지만 이전 연구에서 reordering이 좋은 sample를 위한 inductive bias를 제공하기도 한다고 했었는데, Gaussian Diffusion model은 masking noise보다 자연스러운 gaussian noise를 추가하기 때문에 이런 inductive bias 또한 제공하고 있다고 합니다.

 

게다가 Gaussian diffusion 모델은 "data의 length로도 해석이 가능한" 길이 T가 제약되지 않으므로, sampling 속도를 위해 "더 짧아 질 수도" 있거나 sample의 표현력을 위해 "더 길어 질 수도" 있다고 하고 있습니다.

 

• Interpolation

source image $x_0$가 있을 때, stochastic encoder q()를 활용해 sampling한  $x_t$를 아래와 같이 만들어  줍니다.

$$\begin{matrix}
{x_0}'\sim q(x_0) \\
{x_t}'\sim q(x_t|x_0)
\end{matrix} $$

이후에 아래와 같이 latent를 linear interpolation 했습니다.

$$\bar{x_t}=(1-\lambda )x_t + \lambda {x_t}'$$

그 다음 아래와 같은 식을 통해서 reverse process를 통과시킬 수 있습니다. 

$$\bar{x_0}\sim p(x_0|\bar{x_t})$$

결과적으로 아래그림은 CelebA-HQ의 256x256 image를 다양한 λ에 따라 interpolation하고 reconstruction한 결과입니다. 이런 과정이 아래 그림과 같이 기존 이미지의 인공적인 부분을 linearly interpolate를 통해 없애는 과정이라고 보았습니다.

[CelebA-HQ 256x256 results]

-----------------------------------------------------------------------------------------------------

 

<이후의 트렌드>

• Tackling the Generative Learning Trilemma with Denoising Diffusion Gans(ICLR’22)
  
  • 빠르게 Sampling 하기 위해서 reverse process를 conditional GAN을 활용
• Score-based generative modeling in Latent Space (NIPS’21)
• High-Resolution Image Synthesis with Latent Diffusion Models (CVPR’22)
  
  • Image space에서 Gaussian Noise로, Gaussian Noise에서 Image Space로 Dimension이 너무 크다.
  • Image를 Latent space를 보내고, Latent space에서부터 score-based활용해 두 가지 섞기
  • “Stable Diffusion”에서 활용
• Classifier-Free Diffusion Guidance (’21)
  
  • Classifier Guidance를 학습하려면 Classifier가 따로 학습이 필요하고, Gradient도 구해야하고…
  • Training 과정에서 Classifier Guidance 모델을 같이 학습하다가 점점 줄이는 방식으로 학습
  • Conditonal Sampling
• Cascaded Diffusion Models for High Fidelity Image Generation(’21)
  
  • resolution 작은 이미지를 생성해놓고 점점 키워나가면서 샘플링 하는 방식
• GLIDE : Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models (OpenAI’21)
  
  • Text-Guided로 Image를 만들어내는
  • CLIP Guidance
  • Diffusion의 시작
• DALL-E2 : Hierarchical Text-Conditional Image Generation with CLIP Latents
  
  • GLIDE를 발전시킨 것
  • Diffusion을 사용했지만, Latent Space에서의 Diffusion을 채용했다.
  • text encoder의 값을 가지고 다른 latent를 만들고 그 다음부터 샘플링
• Imagen : Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding (Google, arxiv’22)
  
  • 역시 text를 가지고 Image 생성하는 것
• Diffusion Autoencoders : Toward a Meaningful and Decodable Representation (CVPR’22)
  
  • 다른 architecture와 합치는 방향
  • 이미지에서 semantic encoder로 latent vector를 만들고, 이것을 condition을 줘서 학습
• Image Super-Resolution Via Iterative Refinement (‘21)
  
  • Super Resolution에 쓰인 것
    ** super Resolution : 해상도를 복원하는것
    ** super pixel : pixel을 관련있는 것끼리 뭉탱이로 합치는 것
  • Resolution낮은 것을 Condition을 줘서 생성하는 방법
• Image to Image Diffusion Models (’22)
  
  • Colorization(색깔 주기), Inpainting(중간에 그리기) Uncropping(Crop제거), JPRG Restoration(복원) 모두 SOTA
• ILVR : Conditioning Method for Denoising Diffusion Probabilistic Models (ICCV’21)
  
  • Sampling을 Condition을 어떻게 줘서 샘플링 하면 좋을까?
  • 서울대 논문
• Label-Efficient Semantic Segmentation With Diffusion Models (ICLR’22)
  
  • segmentation을 Diffusion모델을 활용
• SDEdit : Guided Image Synthesis and Editing with Stochastic Differential Equations (ICLR’22)
  
  • 사람이 어느정도 색감을 주면 Noise를 씌웠다가 De-noise해서 실제 realistic 이미지를 만드는 것
• Diffusion Models for Adversarial Purification(ICML’22)
  
  • Adversarial LR 에서도 Attack을 막기 위해 쓰는 것, Noise 입혔다가 다시 씌우기
• Video Diffusion Models (‘22)
• Flexible Diffusion Modeling of Long Videos (arxiv’22)
• Diffusion Probabilistic Modeling for Video Generation (‘22)
• Diffusion Models for Video Prediction and Infilling (‘22)
• MCVD : Masked Conditional Video Diffusion for Prediction, Generation, and Interpolation (arxiv’22)
  
  • Video Generation 에도 쓰인다
• 3D Shape Generation and Completion Through Point-Voxel Diffusion(ICCV’21)
• Diffusion Probabilistic Models for 3D Point Cloud Generation (CVPR’21)
  
  • 3D공간에서 3D Point Cloud를 만들어내는 방법
• Mask GIT : Masked Generative Image Transformer (CVPR’22)
• ImageBART : Bidirectional Context with Multinomial Diffusion for Autoregressive Image Synthesis (NIPS’21)
  
  • Continuous하지 않고 Discrete하게 Diffusion 모델을 학습하는 방법 (Grid형태로)

-----------------------------------------------------------------------------------------------------

 

---

후기 : DDPM은 High Quality Sample을 만들어내기 위한 임팩트 있는 논문이지만, 기존의 nonequilibrium thermodynamics논문에서 diffusion 기법을 "잘 활용해서 실용성있게 만들었다" 정도로 해석할 수 있을 것 같습니다.

 

http://dmqm.korea.ac.kr/activity/seminar/411

https://taeu.github.io/paper/deeplearning-paper-vae/

https://simpling.tistory.com/34

https://gaussian37.github.io/dl-concept-vae/

https://velog.io/@hong_journey/VAEVaritional-Auto-Encoder%EB%A5%BC-%EC%95%8C%EC%95%84%EB%B3%B4%EC%9E%90

https://process-mining.tistory.com/161

https://velog.io/@dbj2000/VAE%EC%9D%98-%EC%9D%B4%ED%95%B4

https://www.youtube.com/watch?v=uFoGaIVHfoE