2025. 4. 30. 22:59ㆍDevelopers 공간 [SOTA]
- Paper : https://arxiv.org/pdf/1901.03416
- Authors
- Deepmind, ICLR’19
- Main Idea
- VAE의 ELBO training objective를 바꾸거나 decoder를 약화하지 않고 posterior collapse문제를 해결합니다.
- ELBO KL term의 하한선을 구하고, contraint를 제공함으로써, Latent가 Decoder에 정보를 제공할 수 있도록 합니다.
- Tasks : Random 2D Image Generation, Random Text Generation
- Results : CIFAR-10, ImageNet(32x32), LM1B
<구성>
0. Before Start...
a. VAE
b. Posterior Collapse
1. Problem
2. Approach
a. Committed Rate
b. Anti-Causal Encoder Network
c. Posterior Holes Problem
3. Results
a. Setting
b. Results
글효과 분류1 : 논문 내 참조 및 인용
글효과 분류2 : 폴더/파일
글효과 분류3 : 용어설명
글효과 분류4 : 글 내 참조
글효과 분류5 : 글 내 참조2
글효과 분류6 : 글 내 참조3
0. Before Start...
논문 설명에 시작하기에 앞서 기본적으로 알고 있어야할 것들에 대해 짚고 가겠습니다.
a. VAE
VAE는 encoder와 likelihood 모델인 decoder $p_\theta(x|z)$로 이루어져있고, 이 중에 특히 decoder는 true distribution $p(x)$를 생성해내도록 학습하는 것이 목적입니다.

VAE는 실제 데이터의 true distribution $p(x)$를 생성하는 것이 목적인데, 학습한 모델이 생성한 분포 $p_\theta(x)$가 이 true distribution과 비슷해야합니다.
모델이 생성한 분포 $p_\theta(x)$는 “x라는 input을 통해 학습한 모델이 생성한 확률분포”인데, 이 x에다가 정확한 값을 넣는다고 생각하면 $p_\theta(x)$는 “x라는 output을 만들어낼 수 있는 모델의 확률”로 해석할 수도 있습니다.
** input과 output이 같기 때문에
그럼 이 “x라는 output을 만들어낼 수 있는 모델의 확률”을 최대화하는 것, 즉 $p_\theta(x)$를 최대화하는 것이 우리의 목적입니다.
이제 목적이 확실하니 $p_\theta(x)$를 임의의 latent distribution $z$에 대한 적분(marginalization) 형태로 표현해보겠습니다.
$$p_\theta(x)= \log \int_z p_\theta(x, z) \, dz=\int_z{\color{red}p_\theta(x|z)}p_\theta(z)\mathrm{d}z$$
이는 아래의 이유로 계산이 불가능(intractable)합니다.
- latent distribution인 $z$ 분포에 대해 알지도 못하는데 이를 적분한다는 것은 말이 안된다.
- latent distribution인 $z$ 분포는 고차원 연속공간에 정의되는데 적분으로 풀낼 수 없다.
- 빨간 부분은 Decoder를 의미하는데, 복잡한 NN의 적분은 불가능합니다.
사실 애초에 latent distribution $z$를 알고 있으면 그냥 latent distribution에서 sampling하도록 학습하면 되므로 이런 과정을 겪고 있는 “원인”이죠.
$p_\theta(x)$를 임의의 latent distribution $z$와 함께 bayes rule로 표현해보겠습니다.
$$p_\theta(x)=\frac{{\color{red}p_\theta(x|z)}p_\theta(z)}{\color{blue}p_\theta(z|x)}$$
이 중에 $p_\theta(z)$는 우리가 임의의 가정을 통해 “Gaussian 분포와 같다”등으로 가정할 수 있다면, encoder의 역할로 보이는 ${\color{blue}p_\theta(z|x)}$만 알아내면되는데, latent 분포를 가정한다 하더라도 역시나 "$x$를 알때 $z$를 어떤 확률로 생성해낼 수 있을지"는 알수가 없습니다.
즉, ${\color{red}p_\theta(x|z)}$는 decoder NN이니까 그값이라도 얻어낼 수 있지만 ${\color{blue}p_\theta(z|x)}$는 위 decoder NN의 역확률이기 때문에 알아낼수가 없다는 것입니다.
그래서 비슷한 분포를 가지는 $q_\phi(z|x)$라는 네트워크를 따로 두고 학습을 진행하고, 이를 encoder라고 부릅니다.
** Variational Inference(변분 추론) 기법이라고 불립니다.
** 기존의 Variational Inference 처럼 데이터 포인트 $x^{(i)}$마다 최적의 $q(z \mid x^{(i)})$를 찾는 것이 아닌 모든 데이터의 공통된 하나의 함수 $q_\phi(z \mid x)$를 학습하기 때문에 Amortized(비용 분산) Variational Inference 라고 부르기도 합니다.
** 당연히 이 encoder는 ${\color{red}p_\theta(x|z)}$로 근사할 예정입니다.
위 과정을 단순화한 그림입니다.

여기까지는 marginal likelihood $p_\theta(x)$를 최대화하는 우리의 목적을 위한 수식에서 intractable한 부분들을 대체하는 과정을 거쳤는데, 이젠 그 수식을 정확하게 풀어나가 보겠습니다.
먼저 이 수식을 최대화하기 위해, 하한선(lower bound)을 만들고 “적어도 이 하한선을 크게 만들면 실제 값은 높아질 것이다”라고 하는 Lower Bounding Technique방법을 선택합니다.
** log는 log-likelihood로 진행하기 위함입니다.
$$\mathcal{L}(x;\theta)\leq log\,p_\theta(x)$$
그럼 하한선인 $\mathcal{L}(x;\theta)$ 알아내기 위해 $log\,p_\theta(x)$식을 아래와 같이 풀어나갑니다.
$$ \begin{matrix}
\textrm{log}p_{\theta }(x) = \textrm{log}p_{\theta }(x)\int q_{\phi }(z|x)dz\:\:\:(\because \int q_{\phi }(z|x)dz = 1)\\
= \textrm{log}\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)}\int q_{\phi }(z|x)dz\:\:\:(\because p_{\theta }(x)=\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)},\: bayes\:rule) \\
= \int \textrm{log}\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)}q_{\phi }(z|x)dz\:\:\:(\because Evidence\:Into\:Integral) \\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)}]\:\:\:(\because Monte\:Carlo\:Approximation) \\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{p_{\theta }(z|x)}\frac{q_{\phi }(z|x)}{q_{\phi }(z|x)}]\:\:\:(\because Multiple\:By\:1) \\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{q_{\phi }(z|x)}]+\mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{q_{\phi }(z|x)}{p_{\theta }(z|x)}]\:\:\:(\because Split\:the\:Expectation) \\
= \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{q_{\phi }(z|x)}]+D_{KL}[q_{\phi}(z|x)||p_{\theta }(z|x)]\:\:\:(\because Definition\:of\:KL\:Divergence)\\
\geq \mathbb{E}_{q_{\phi }(z|x)}[\textrm{log}\frac{p_{\theta }(x,z)}{q_{\phi }(z|x)}]\:\:\:(\because KL\:Divergence\:always\:\geq 0, ELBO)\\
\end{matrix}$$
마지막을 보면, 결국 위 값은 특정 어느 값 보다 크거나 같다고 표현되고 결국 이 값이 하한선이 되며 이 값을 ELBO(Evidence Lower Bound)라고 부릅니다.
$$\begin{aligned}
\mathcal{L}(x;\theta)&=\mathbb{E}_{q_\phi(z|x)}[log\,p_\theta(x,z)-log\,q_\phi(z|x)]\\
&=\mathbb{E}_{q_\phi(z|x)}[log\,p_\theta(x|z)]-D_{KL}(q_\phi(z|x)\|p_\theta(z))
\end{aligned}$$
위는 "확률분포로 포함된 수식적으로 설명된 함수"이고 "실제 Loss"는 아래와 같습니다. 최대값을 구하는 것이기 때문에 "음수의 최소값"을 구하도록 바꾸고, 수식을 현실 구현 가능하도록 수정합니다.

따라서 이 ELBO를 크게 만듦으로써 우리가 원하는 목표를 이뤄냅니다.
또한 AE(Auto Encoder)와 VAE(Variational AE)의 차이는 아래와 같습니다.
- Auto Encoder : encoding을 통해 암호화 및 압축 하고 decoding을 통해 복원하는 것이 목적입니다. Latent Vector가 하나의 값입니다.
- Variational(변형) AE : 새로운 것을 생성하는 것이 가능한 Generative Model입니다. Latent Vector가 확률 분포에 기반한 값들입니다.
아래는 MNIST 데이터를 각각 AE와 VAE로 특징 추출한 뒤 표현한 그림인데, AE는 cluster가 넓게 퍼져있고 VAE는 중심으로 잘 뭉쳐져있습니다. 따라서, VAE가 데이터의 특징을 파악하는데 유리하다고 합니다.

이번엔 코드상의 Loss는 어떨까요? 아까 만들었던 수식과 코드를 보겠습니다.
$$Loss=\underset{\phi,\theta}{arg\,min}\sum-{\color{red}\underbrace{\mathbb{E}_{q_\phi(z|x)}[log\,p_\theta(x|g_\theta(z))]}_{Reconstruction\:Loss}}+{\color{blue}\underbrace{D_{KL}(q_\phi(z|x)\|p_\theta(z))}_{KL\:Divergence}}$$
reconst_loss = F.binary_cross_entropy(x_reconst, x, reduction='sum')
kl_div = 0.5 * torch.sum(mu.pow(2) + logvar.exp() - logvar - 1)
loss = reconst_loss + kl_div
이외 따로 설명하지 않은 부분이 하나 있는데, "정규분포 z에서 샘플링하는 것"을 구현하기 위해 평균과 분산을 구해내고 “평균 +noise*분산”으로 표현해내는 Reparametrization Trick을 활용합니다.
b. Posterior Collapse
먼저 위에서 정의된 용어들을 다시 살펴보겠습니다.
- Latent 관련
- $p(z)$ : prior
- Decoder 관련
- $p_\theta(x|z)$ : likelihood(decoder)
- $p_\theta(x)$ : marginal likelihood
- Encoder 관련
- $p(z|x)$: true posterior
- $q_\phi(z|x)$ : approximate posterior(encoder)
따라서 VAE의 최종목적은 아래와 같습니다.
- approximate posterior(encoder)가 true posterior와 비슷해지도록
- marginal likelihood를 최대화
따라서 ELBO는 아래와 같았습니다.
$$\mathcal{L}_{ELBO}=\underbrace{\mathbb{E}_{q_\phi(z|x)}[log\,p_\theta(x|z)]}_{Reconstruction\,term\,(Decoder\,Training)}-\underbrace{D_{KL}(q_\phi(z|x)\|p(z))}_{Regularization\,term\,(Convergence\,to\,Prior)}$$
보이는 것과 같이 아래의 두가지 term으로 구분됩니다.
- Reconstruction term : 데이터 $x$가 $z$를 통해 얼마나 잘 복원되는가
- Regularization term (KL term) : posterior $q_\phi(z|x)$가 prior $p(z)$와 얼마나 가까운가
이 중에 KL term은 애초에 $p(z)$에 가까워지도록 "정보량이 적은 Latent"로 유도되기 때문에, Posterior Collapse라는 문제가 발생하기도 합니다.
즉, 위와 같이 Loss를 만들었으니 당연한 결과일 수도 있지만, 애초에 $p(z)$를 Isotropic Guassian $\mathcal{N}(0,1)$으로 가정했는데 이 분포 자체가 "너무 간단한 분포"여서, $q_\phi(z|x)$가 굉장히 rich한 분포를 학습해야함에도 불구하고 복잡한 데이터 구조를 잘 표현하지 못해서 아래와 같은 현상들이 일어나는 문제입니다.
- Generated sample의 다양성 저하 : $z \sim p(z)$로 샘플링해도 Latent에 의미 있는 정보가 없어 대부분 비슷한 $x$를 생성
- Generated sample의 품질 저하: Latent에 정보가 없어 Reconstruction은 가능하지만 downstream task (예: clustering, classification)에 활용시 성능 낮음
이는 다른 방향으로 해석되기도 하는데, decoder가 $z$의 정보를 활용하지 않고도 복원을 할 수 있는 바람에, Latent $z$가 무의미한 랜덤 변수가 되어 버리는 것이 원인이라고 보기도 합니다.
이런 원인으로 인해, 아래 두가지 네트워크에서는 이 현상이 두드러지게 발생합니다.
- CVAE(Conditional VAE) : "조건 c"가 충분히 informative해서, decoder가 조건 c만으로 생성이 가능해집니다.
- Autoregressive VAE : "바로 전 pixel" 혹은 "바로 전 token"이 충분히 informative해서, decoder가 autoregressive한 생성만으로 가능해집니다.
---------------------------------------------------------------
<Posterior Collapse 원인 재정리>
더 정확한 원인을 정리해보면 posterior collapse란, posterior인 $q_\phi(z|x)$가 너무 약하거나(too weak) 너무 지저분할때(too noisy)할 때 decoder가 z를 무시하게 되면서 생기는 현상입니다.
즉, $q_\phi(z|x)=\mathcal{N}(\mu,\sigma^2)$라고 할 때, 아래와 같은 두가지 원인입니다.
- too weak : 위 $\mu,\sigma$가 $q_\phi(z|x)\simeq q_\phi(z)=\mathcal{N}(c_1, c_2)$와 같이 input과 무관한 constant 분포로 전락하기 때문에 decoder가 이를 통해 만들어진 $z$값을 무시
** 즉, $x$가 달라도 샘플링되는 $z$의 분포는 거의 변하지 않고, $z$는 $x$에 대한 정보를 담지 못합니다.
** 원래는 $x$에 따라 "$z$의 분포"가 달라져야합니다. - too noisy : 위 $\mu,\sigma$가 unstable하기 때문에 decoder가 이를 통해 만들어진 $z$값을 무시
** $\mu,\sigma$가 unstable하다는 것은 $\sigma$가 크거나, $\mu,\sigma$가 $x$에 따라 무관하게 출력되는 현상입니다.
두 경우 모두 decoder는 결국 $z$ 정보를 무시하고 reconstruction을 하게 되는 것입니다.
---------------------------------------------------------------
이런 Posterior Collapse를 해결하기 위해, 이를 Distangle하기 위한 다양한 기존의 시도들이 있었습니다.
** Disentanglement : "조건"을 무시하도록 하는 과정
- 1. Autoencoder 구조 개선 : VampPrior, Hierarchical VAE, VQ-VAE, Implicit-LVM
** [VampPrior] VAE with a VampPrior(PMLR ’18)
▶ richer하고 유연한 prior로 expressive한 z 공간 유지
** [Hierarchical VAE] Ladder Variational Autoencoders (NIPS’16)
** [Hierarchical VAE] NVAE: A Deep Hierarchical Variational Autoencoder (NIPS’20)
▶ Hierarchical한 Latent 구조를 도입해, 정보 표현의 풍부함을 증가
** [VQ-VAE] Neural Discrete Representation Learning (NIPS’17)
▶ KL 항 대신 코드북을 사용함으로써 posterior collapse가 원천적으로 발생하는 것을 막음
** [Implicit LVM] Implicit deep latent variable models for text generation
▶ 조금 더 복잡한 prior distribution을 활용 - 2. NN모델 구조 개선 : Skip-VAE ==> 그림넣기!!!
** [Skip-VAE] Avoiding Latent Variable Collapse with Generative Skip Models (PMLR’19)
▶ 인코더와 디코더 사이에 직접 연결을 추가하여, 정보 손실을 줄임 - 3. KL term개선 : beta-VAE, Free-bits, Delta-vae, KL Annealing
** [beta-VAE] β-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework (ICLR’17)
▶ ELBO의 KL 항에 가중치 $\beta$를 도입하여, $\beta < 1$로 설정함으로써 KL 항의 영향을 조절
** [Free-bits] Improved Variational Inference with Inverse Autoregressive Flow (NIPS’16)
▶ KL을 일정 수준 이하로는 줄이지 않게 함
** [Delta-vae] Preventing Posterior Collapse With δ-VAEs(ICLR’19)
▶ free bits과 유사하지만 좀 더 부드럽게 KL 하한을 두는 방식
** [KL Annealing] Generating Sentences from a Continuous Space (arxiv’15)
▶ 학습 초기에 KL 항의 가중치를 낮게 설정하고 점진적으로 증가시켜, 모델이 잠재 변수를 활용하도록 유도 - 4. Mutual Information 유지/최대화 : InfoVAE
** [InfoVAE] InfoVAE: Information Maximizing Variational Autoencoders (arxiv’17)
▶ VAE 목적 함수에 입력 $x$와 잠재 $z$ 간의 상호정보량 $I(x;z)$를 명시적으로 높이는 항을 추가
아래 그림은 Skip-VAE을 활용했을때 Latent Variable을 clustering한 결과입니다. Skip-VAE의 결과는 VAE보다 Latent Variable들을 잘 클러스터링하는 것을 보아 더욱 의미 있는 표현을 가진다고 볼 수 있습니다.

1. Problem
본 논문에서는 Autoregressive 모델에서의 문제로 시작합니다. 즉, Autoregressive decoder가 너무 expressive해서 data density를 latent variable $z$없이 모델링할 수 있게 되면 posterior가 prior로 collapse됩니다.
다시 말해 아래의 ELBO에서 rate term이 0으로 줄어들게 되면, approximate posterior인 $q_\phi(z|x)$가 prior인 $p_\theta(z)$와 같아지고, latent variable $z$가 결국 input $x$에 대한 아무런 정보도 전달하지 못합니다.
** rate term이 무엇인지에 대해 궁금하시면 아래 더보기를 참조하세요
$$\log p(x) \geq \mathbb{E}_{z \sim q(z \mid x)} \left[ \log p(x \mid z) \right] - D_{\mathrm{KL}}(q(z \mid x) \,\|\, p(z))$$
----------------------------------------------------------------------
<Rate와 Distortion>
Shannon의 Rate-Distortion 이론에서 나온 이 개념은 DDPM와 VAE에서 비슷하게 사용됩니다.
먼저 DDPM에서 사용되는 Varational Bound는 아래 식과 같습니다.
$$\mathcal{L}=\mathbb{E}_q[
\underbrace{D_{\mathrm{KL}}(q(\mathbf{x}_T \mid \mathbf{x}_0) \,\|\, p(\mathbf{x}_T)) }_{L_T}
+ \sum_{t>1} \underbrace{D_{\mathrm{KL}}(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) \,\|\, p_\theta(\mathbf{x}_{t-1}\mid \mathbf{x}_t)) }_{L_{t-1}}-\underbrace{\log p_\theta(\mathbf{x}_0 \mid \mathbf{x}_1) }_{L_0}
]$$
위는 아래 두가지로 나눠볼 수 있습니다.
- $\mathcal{L}_1+\dots+\mathcal{L}_T$ (Rate) : 중간 KL terms은 모델이 각 timestep마다 얼마나 정보를 보존하며 복원 가능한지를 측정합니다. 즉, latent trajectory가 얼마나 많은 정보를 보존하고 있는지의 누적량입니다.
- $\mathcal{L}_0$ (Distortion) : Reconstruction Loss인 이 항은 노이즈 제거 프로세스의 최종 출력이 얼마나 원본과 가까운지를 측정합니다.
다음으로 VAE에서 사용되는 Evidence Lower Bound(ELBO)는 아래 식과 같습니다.
$$\mathcal{L}=\log p(x) \geq \mathbb{E}_{z \sim q(z \mid x)} \left[ \log p(x \mid z) \right] - D_{\mathrm{KL}}(q(z \mid x) \,\|\, p(z))$$
위는 아래 두가지로 나눠볼 수 있습니다.
- KL divergence (Rate) : 얼마나 많은 정보를 latent variable $z$에 encode하고 있는지를 정량화합니다. 즉, latent를 표현하기 위해 평균적으로 얼마나 많은 정보 (bits 또는 nats)가 필요한지를 측정합니다.
- Reconstruction term (Distortion) : decoder가 $z$를 보고 얼마나 정확하게 $x$를 재구성했는지를 측정합니다.
두 모델 정보 이론에서의 Rate(정보 보존량, Code Length, 압축률)개념을 차용했으며, 이들은 모두 "데이터를 재구성하기 위해 평균적으로 얼마만큼의 정보를 latent 혹은 noise 제거 경로를 통해 보존해야 하는가"를 나타내는 정보량의 측정 단위로 활용됩니다.
반대로 Distortion은 복원된 데이터가 원본 데이터와 얼마나 다른지 측정하는 양입니다.
- DDPM : 원본 $x$와 복원 $\hat{x}$ 간의 차이
- VAE : decoder가 $z$를 보고 얼마나 정확하게 $x$를 재구성했는지를 측정
결국 "이 둘의 Tradeoff"를 활용해 정보 이론에서 핵심적으로 다루는 것은 “얼마나 적은 정보로(rate) 원본을 얼마나 정확히(distortion) 재현할 수 있는가?”입니다.
----------------------------------------------------------------------
따라서 결국 우리가 원하는 것 처럼 representation이 의미 있으려면 rate term이 positive로 유지되어야 한다고 주장합니다.
기존 논문들은 이 문제를 해결하기 위해서 ELBO training objective를 변경하거나 decoder를 약하게 만들어버리지만, 이는 굉장히 hyperparameter에 민감하기 때문에 어렵기도 합니다.
2. Approach
이 논문에서는 ELBO training objective를 바꾸거나 decoder를 약화하지 않고, structural contraints를 제안함으로써 posterior collapse문제를 해결합니다.
즉, approximate posterior인 $q_\phi(z|x)$와 prior인 $p_\theta(z)$의 distribution famility를 고르고, 아래와 같은 $\delta$ 하한선을 제안합니다.
**본 논문에서는 이를 모델의 "Committed Rate"라고 부릅니다.
$$min_{\theta, \phi}\,D_{KL}(q_\phi(z|x)\|p_\theta(z))\geq {\color{red}\delta}$$
그럼 이 $p_\theta$와 $q_\phi$의 분포를 어떻게 골랐는지 자세히 살펴보겠습니다.
a. Committed Rate
Speech & Natural Language & Text 등 에서는 강한 spatio-temporal continuity 특징을 보입니다.
본 논문에서는 이런 sequencial setting에서 $\delta$-VAE를 구성하기 위해 아래와 같은 셋팅을 진행합니다.
1. approximate posterior $q_\phi(z|x)$
"시간적으로 독립적인" mean-field posterior를 구성합니다.
$q(\boldsymbol{z}_t|\boldsymbol{x})=\mathcal{N}(\boldsymbol{z}_t ;\mu_t(\boldsymbol{x}),\sigma_t(\boldsymbol{x}))$
당연히 이 mean-field posterior는 아래서 설명할 "각 시간의 prior"과는 연관이 있습니다.
2. prior $p_\theta(z)$
prior은 아래와 같이 AR(1)으로 구성됩니다.
**AR(1) : 1차 linear한 Auto Regressive process
** $\epsilon_t$ : constant variance $\sigma^2_\epsilon$ 를 가지는 zero-mean Guassian noise입니다.
$$\begin{aligned}
\boldsymbol{z}_t&=\alpha\boldsymbol{z}_{t-1}+\epsilon_t,\,\,\,\epsilon_t\sim\mathcal{N}(0,\sigma^2_\epsilon)\\
p(\boldsymbol{z}_t|\boldsymbol{z}_{<t})&=\mathcal{N}(\boldsymbol{z}_t;\alpha \boldsymbol{z}_{t-1},\sigma_\epsilon)
\end{aligned}$$
이때 $|\alpha|<1$하면, 이 프로세스가 WSS하게 유지되고 평균 0와 분산 $\frac{\sigma^2_\epsilon}{1-\alpha^2}$가 됩니다.
** WSS(Wide-Sense Stationary) : random process에서 쓰이는 용어로, random process $x(t)$의 평균이 항상 같고 auto correlation은 시간차에만 의존하는 것을 의미하고, 아래의 조건을 모두 만족해야합니다.
$$\begin{aligned}
E[x(t_1)]&=E[x(t_2)]&&=\mu&&\,\,Mean\\
Cov(x(t_1),x(t_2))&=E[(x(t_1)-\mu)(x(t_2)-\mu)]&&=R(t_2-t_1)&&\,\,Auto\, Correlation
\end{aligned}$$
위와 같이 평균 0와 분산 $\frac{\sigma^2_\epsilon}{1-\alpha^2}$라면, 편리하기 위해 본 논문에서는 $\sigma_\epsilon=\sqrt{1-\alpha^2}$를 유지합니다.
위와 같이 셋팅하고 나면, prior와 posterior사이의 mismatch라고 할 수 있는 “KL-divergence의 하한선”이 아래와 같이 생깁니다.
- d: 각 시점에서의 latent variable의 차원 수
- n: 시퀀스의 길이 (예: 음성의 프레임 수)
- $\alpha_k$ : 각 latent 차원 k에 대한 AR(1) prior의 자기회귀 계수
$$D_{KL}(q(z|x)\|p(z))\geq \frac{1}{2}\sum^d_{k=1}(n-2)ln(1+\alpha^2_k)-ln(1-\alpha^2_k)$$
결과적으로 앞서 언급된 Committed Rate를 찾은 것이죠. 아래는 prior sqaured correlation인 $\alpha$와 sequence length n에 따른 KL divergence의 하한선이라할 수 있는 $\delta$의 크기를 보입니다.

또한 아래는 $\alpha$에 따른 $\delta$-VAE의 2D optimal posterior와 2D prior를 보입니다.
** 파란색은 prior, 빨간색은 posterior
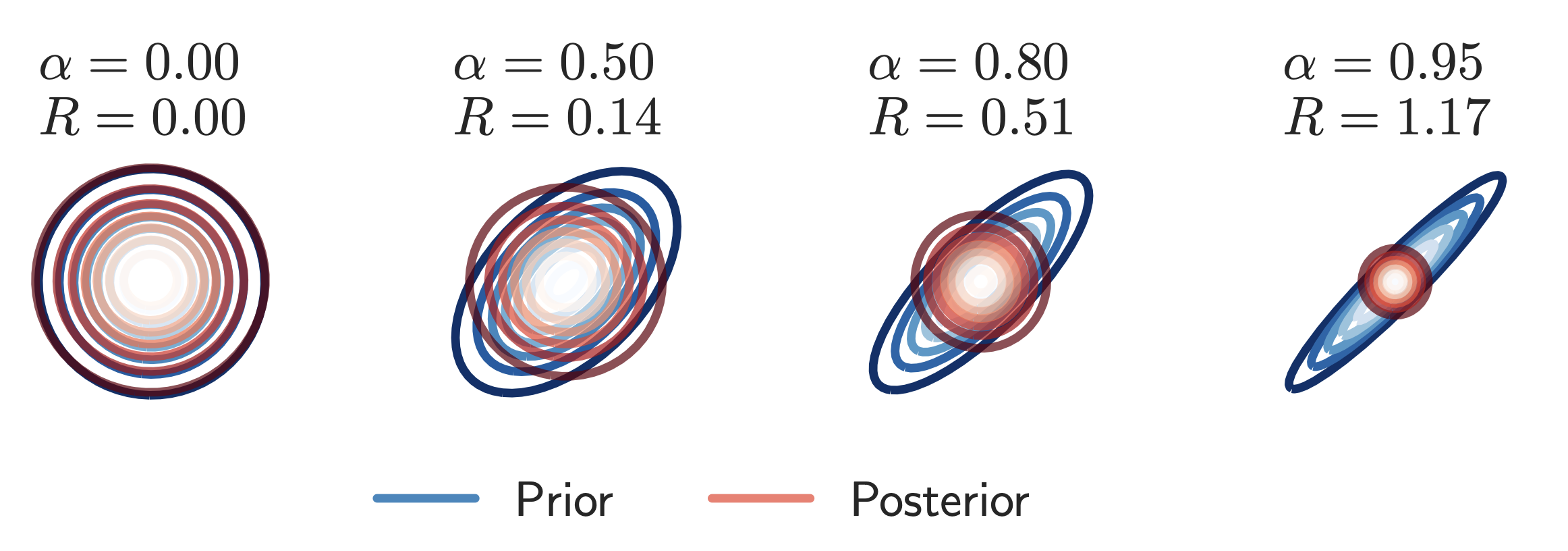
위 두 결과를 보면 아래와 같이 정리할 수 있습니다.
- $\alpha$가 작을수록 : prior와 posterior의 분포가 비슷해지고, (KL 하한선=0)
- $\alpha$가 클수록 : prior는 더 강한 auto correlation을 가지면서, optimal posterior와 모양도 달라지고 KL하한선도 증가합니다. 즉, 정보를 더 많이 보낼 수 있는 통로가 확보됩니다.
또한, 앞서 시간에 따라 AR(1) prior을 사용했다고 했는데, 여기서 사용되는 파라미터를 활용해 latent space상의 "temporal correlation의 degree"를 제어할 수 있다고 볼 수도 있습니다. 즉, 아래와 같습니다.
- $\alpha$가 1에 가까울수록 : latent의 시간에 따른 변화가 점점 느려지고, prior trajectory가 부드러워집니다.
- $\alpha$가 0에 가까울수록 : prior가 i.i.d. Gaussian이 되어 시점 간의 상관이 사라집니다.
** i.i.d. : Independent and Identically Distributed으로 여기서는 Independent Standard Gaussian을 의미합니다.
또한 "시간에 따라 독립적인 posterior"와 "correlated된 Prior"는 시간적으로 느린 변화량을 가지는 SFA와 연관이 되어있다고 합니다.
** SFA(Slow Feature Analysis) : Spatio-Temporal하게 크게 변화하지 않는 features를 학습하기 위한 Unsupervised 학습법입니다.
즉, $\alpha$가 1에 가까울수록 latent의 시간에 따른 변화가 점점느려지므로 slow feature처럼 동작합니다. 이런 구조가 SFA와 비슷하다고 합니다.
b. Anti-Causal Encoder Network
$p(\boldsymbol{x}_t|\boldsymbol{x}_{<t})$를 이미 정확하게 estimate하는 decoder를 가지는 것을 high-capacity autogressive network라고 합니다.
근데 이런 경우는 어떤 보충정보를 줘서 posterior collapse를 방지할 수 있을까요?
본 논문에서는 아래와 같은 방법들은 좋지 않다고 생각합니다.
- "과거의 encoding정보들"을 제공하는 것은 decoder가 과거 정보에 대해 이미 접근할 수 있었기 때문에 무의미합니다.
- 아래식과 같이 해당 시점의 timestep에만 조건부 독립적인 conditional로 주는 것은 DPI에 의해 decoder는 이미 알고 있으니까 더 줄 정보가 따로 없습니다.
즉, latent variable인 $\boldsymbol{z}_t$를 제공해도 이미 autoregressive하게 $\boldsymbol{x}_t$를 잘 예측할 수 있으므로, 장점이 없다는 것입니다.
** DPI(Data Processing Inequality) : 정보이론의 기본 원리로, 정보는 가공되거나 중간 변수를 거치면서 더 늘어날 수 없으며, 오히려 구별하기 어려운 상태로 손실될 수 있다는 사실을 의미합니다.
$$p(\boldsymbol{x}_t|\boldsymbol{z})=p(\boldsymbol{x}_t|\boldsymbol{z}_t)$$
따라서, 본 논문에서는 $\boldsymbol{z}_t$에 $\boldsymbol{x}_{\geq t}$에 대한 encoding 정보를 담아서 decoder에게 전달한다면, decoder가 mutual information에 대한 KL cost를 한번 제공하면서도 미래 예측에 대한 entropy도 줄일 수 있다고 합니다.
따라서 미래 timestep에 대한 latent를 만들어내는 생성이 가능하도록 아래 그림과 같은 Anti-Causal Encoder구조를 제안합니다.

** Causal의 뜻이 궁금하시면 아래 더보기를 참조하세요
----------------------------------------------------------------------
<Causal의 뜻>
causal은 원인관계를 의미하지만 그 중 시간적 원인 관계(Temporal Causality)를 따르는 정보 구조를 주로 의미합니다.
본 논문에서 정의하는 Anti-Causal 구조와 Non-Causal구조는 아래와 같습니다.
- Anti-Causal (인과적) 구조 : 현재 timestep $z_t$ 를 추론할 때 과거의 $x_{<t}$에는 접근할 수 없고, 미래의 $x_{\geq t}$만 사용
** 일반적으로 “causal”은 과거만 보는 구조지만, $\delta$-VAE에서는 오히려 미래만 보는 구조이므로 anti-causal이라고 부릅니다. - Non-Causal (비인과적) 구조 : 모든 시점의 observation $x_{1:T}$을 사용해서 모든 $z_t$를 $q(z_t|x_{1:T})$형태로 추론
많이 듣는 Causal Attention에서의 “causal”은 "원인 → 결과의 시간 흐름을 제한한다"는 점에서 비슷한 개념으로 사용됩니다.
이 목적을 위해 Causal Attention은 attention 계산시, 현재 시점보다 미래 시점의 정보를 보지 못하도록 제한하는 메커니즘입니다.
왜냐하면 Autoregressive generation에서는 미래를 보게 하면 반칙이기 때문에 이전 정보만 보고 현재를 예측해야 하기 때문입니다.
----------------------------------------------------------------------
즉, 위와 같은 구조를 통해 Encoder, 즉 variational posterior는 과거의 timestep에 의존할 수 없고, 미래 관측치로부터만 latent를 만들어냅니다.
결과적으로는 encoder는 모든 시점 관측치를 보고 latent를 만들어내며, 시간순서를 고려하지않는 encoder와 decoder를 만들어냅니다.
실제 anti-causal은 non-causal구조의 subgraph인데, 실제 실험해보니 anti-causal구조가 더 우수한 성능을 보이는 경우가 많았다고 합니다.
c. Posterior Holes Problem
다루지 않은 문제 중에 Posterior Holes 문제가 있습니다.
이는 prior $p(z)$와, 아래 식과 같은 aggregate posterior $q_\phi(z)$가 있을 때,
$$q_\phi(z)=\mathbb{E}_{x\sim D}[q_\phi(z|x)]$$
이 둘의 차이가 커짐으로써, "aggregate posterior가 probability density를 만들어내지 않은 영역에 대한 prior distribution을 decoder가 활용하는 현상"이 발생합니다.
즉, 이전에 학습하지 않은 latent 영역이 사용되면서 VAE의 성능이 낮아집니다.
이 현상은 $\delta$-VAE에서 더 악화되는데, 본 논문에서는 prior와 posterior간의 mismatch를 유도하기 때문에 prior와 aggregate posterior간의 mismatch가 발생하기 때문입니다.
이를 해결하기 위해 기존 논문에서는 variational family의 복잡도를 향상시킴으로써 해결했지만, objective를 바꿈으로써 KL term을 수정하는 것은 본 논문의 목적이 아닙니다.
** "variational familiy의 복잡도를 증가시켰다"는 것은 approximate posterior인 $q_\phi(z|x)$를 더 표현력이 풍부한 분포를 가지도록 설계한다는 뜻인 것 같습니다.
따라서 본 논문에서는 VQ-VAE에서 적용한 것과 같은 “보조(Auxiliary) prior”를 aggregate posterior와 매칭시키기 위해 사용합니다.
** [VQ-VAE] Neural discrete representation learning (arxiv’17)
간단한 Autoregressive 모델을 위한 “보조(Auxiliary) prior”인 $p^{aux}$를 (1-layer LSTM+ conditional Gaussian)의 출력으로 사용합니다.
3. Results
다시한번 본 논문의 목적을 살펴보자면 아래와 같습니다.
- Latent Variable 모델의 Density를 모델링함으로써 Representation를 학습
- powerful한 Decoder를 활용하는 것
이 목적을 위해 제안된 위 방법들의 실험 결과를 살펴보겠습니다.
a. Setting
먼저 Image와 관련된 셋팅은 아래와 같습니다.
- Model :
- Decoder : PixelSNAIL구조 기반 + GatedPixelCNN의 요소를 차용한 autogressive 모델
- ≒ PixelSNAIL, PixelCNN++ : 하나의 채널이 discretised mixture of logistics distributions를 생성하도록 합니다. 단, RGB채널간에는 linear한 dependencies가 존재합니다.
- ≒ PixelSNAIL : attention layers + masked Gated-Conv layer
- ≒ GatedPixelCNN : Gated Conv 구조
- Attention : 기본 Multi-head Attention
- Decoder Condition : 1x1 conv를 활용하는 PixelCNN과는 다르게 encoder output에 대한 attention을 적용하며, 앞서 설명한 anti-causal 구조도 적용합니다.
- Encoder : Decoder와 유사
- 단, Anti-causal구조를 위해 입력에 대해 Reverse/Shift/Crop해 future context에 대한 latent를 구성하도록 했습니다.
- computation을 위해 "각각의 pixel에 대한 latent"가 아닌, "각 row에 대한 multi-dimentional Latent Variable"을 구성하도록 했습니다.
- Decoder : PixelSNAIL구조 기반 + GatedPixelCNN의 요소를 차용한 autogressive 모델
- Data : CIFAR-10, downsampled(32x32) ImageNet
다음으로 Text와 관련된 셋팅은 아래와 같습니다.
- Model : 기본 Transformer구조
- Latent Variables 차원 : sequence길이는 인풋과 동일한 토큰 개수를 갖도록 설계합니다.
- 0.2, 0.4의 $\alpha$를 활용한 2차원의 값을 가집니다.
- 즉, 한 차원은 느리게 (slower) 변하고 다른 차원은 조금 더 빠르게 (less slow) 변하는, 서로 다른 시간적 민감도를 가진 latent로 구성한 것입니다.
- Decoder : 일반적인 Transformer처럼 causal self-attention을 활용했습니다.
- Encoder : anti-causal structure를 활용하기 위해 decoder에서 사용되는 것과 같은 inverted causality mask를 사용했습니다. 이를 통해 현재의 timestep~future timestep 모두를 살펴볼 수 있습니다.
- Latent Variables 차원 : sequence길이는 인풋과 동일한 토큰 개수를 갖도록 설계합니다.
- Data : LM1B
- Tensor2Tensor로 전처리
b. Results
차근차근 결과를 살펴보겠습니다.
1. Density Estimation
Image에 대해 prior work들과 아래 식과 같은 NLL을 활용해 “모델이 얼마나 데이터를 잘 설명하는지”를 비교한 결과는 아래와 같습니다.
** NLL(Negative Log-Likelihood) : ELBO와 관련된 값이며, 값이 작을 수록 모델이 입력데이터 $x$를 더 정확히 설명한다는 뜻입니다.
$$bits/dim=-\frac{1}{D}log_2p_\theta(x)=\int p_\theta(x|z)p(z)\mathrm{d}z$$

먼저 전체적으로는, 예상 한것과 같이 "autoregressive decoder에서 사용한 capacity"가 전체 성능에 큰 영향을 미치는 것을 확인했으며, "latent를 활용하지 않는 autoregressive 모델"과도 상응한 성능을 달성했다고합니다.
ImageNet 32x32에서는 Image Transformer와 비슷한 성능을 보이고, CIFAR-10에서는 SOTA 성능을 보였습니다.
표 중간에 가로()되어있는 부분은 실제 “Latent 가 얼마나 많은 정보를 전달하고 있는지”를 의미하는 실제 아래식과 같은 KL term을 설명합니다.
$$D_{\mathrm{KL}}\left(q_\phi(z \mid x) \;\|\; p(z)\right) = \mathbb{E}_{q_\phi(z \mid x)} \left[ \log \frac{q_\phi(z \mid x)}{p(z)} \right]$$
근데 이 KL 값이 작아보여도 실제로는 유의미한 정보량이라고 합니다. 예를 들어 0.02bits/dim인경우 아래 식과 같이 이미지 하나당 약 61bit의 정보량이 latent에 포함되었다는 것입니다.
$$KL=0.02\times 32\times 32\times 3(RGB)=61.44bits$$
마지막으로 CIFAR10에서 auxiliary prior를 사용했을 때 Latent Code를 더 효율적으로 사용하는 것을 확인할 수 있는데, 같은 performance를 보이면서도 거의 50%의 rate를 줄였습니다. (0.02 → 0.01)
2. Latent Variable의 활용 측정
이번엔 Image에 대해 "Latent Variable이 실제로 데이터의 의미있는 표현을 학습했는지"를 확인해봅니다.
먼저, 아래는 $z$가 생성된 샘플에 얼마나 영향을 미치는지를 조사하기 위해, 보조 prior로부터 샘플링한 고정된 $z$를 condition으로 decoder를 통해 여러번 샘플링한 결과입니다.

배경 색이나 오브젝트의 위치등 global structure는 비슷하지만 디테일이 많이 달라지는 것을 보아, 모델이 latent variable을 통해서는 global 정보를 얻고 autoregressive decoder를 통해 local 정보를 채우는 것으로 보인다고 합니다.
또한 아래는 학습된 latent를 활용해 downstream task에서 얼마나 잘되는지를 정량평가하기 위해, CIFAR-10에 대해 linear classification을 진행한 결과입니다.
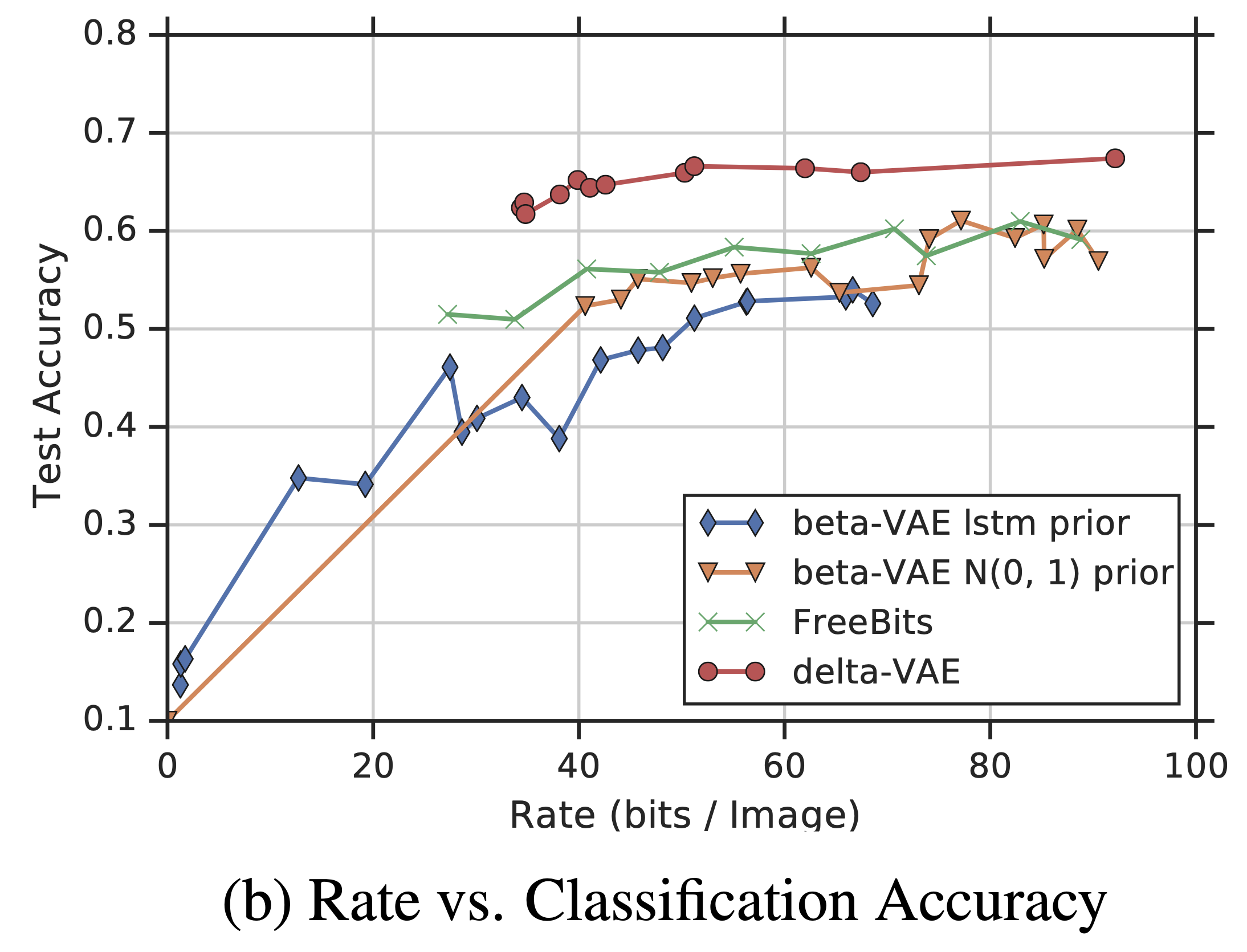
일반적으로 모델의 정해진 rate가 높을 수록 classification 정확도가 높아지는 것을 볼 수 있고, 가장 높은 rate에서는 92bits/image의 정보를 담으면서도 정확도가 69%였습니다. 이는 다른모델에 비해 굉장히 좋은 수치입니다.
하지만 본 논문에서는 "향상된 log-likelihood가 무조건 linear classification 정확도를 향상시키지는 않는 것"을 보아, task를 위해 명확하게 필요한 것은 선형분리가 잘된 feature space라고 이야기합니다.
3. Ablation Studies
posterior collapse를 해결하기 위해 시도했던 다른 모델들과 “latent variables가 이미지에 대해 취득한 정보의 양”을 비교하기 위해 CIFAR-10 데이터셋에서 rate-distortion결과를 보입니다.

위 그림을 보면 $\delta$-VAE는 상대적으로 굉장히 stable하고 density estimation결과가 모든 rate에서 우세한 것을 볼 수 있습니다.
또한 다른 방법 같은 경우 본 논문과 달리 적용하기가 용이하지도 않다고 합니다.
- Linear Annealing : latent variable의 사용성을 높이는 학습을 위해, 굉장히 넓은 범위의 value를 활용하더라도 쉽지 않았으며, $\beta$가 1.0에 달하면 바로 KL이 collapsed 되어버립니다.
- $\beta$-VAE : target rate를 찾기가 어려워 KL이 아예 collapsed되거나 너무 큰 결과가 나와, 정보의 낭비가 커집니다.
- Free-bits : 하이퍼파라미터에 굉장히 민감해 최적화가 어렵습니다.
이와 반해 $\delta$-VAE는, target rate를 $\alpha$를 활용해 명확하게 설계할 수 있으며, 최적화도 overfitting 없이 잘됩니다.
다음으로 아래는 anti-causal encoder구조와 non-causal structure를 CIFAR-10에서 density estimation한 뒤 비교한 결과입니다.
** 논문에는 나와 있지 않지만 NLL(KL term)값을 구한 것 같습니다.
** $l$: number of layers
** $h$: hidden size,
** $a$: number of attention layers

결과는 아래와 같이 정리됩니다.
- decoder가 powerful하지 않을때(6-layer PixelCNN, no attention) : anti-causal 구조가 non-causal만큼은 잘 동작하지 않았습니다.
- decoder가 powerful해지면(attention 추가, layer 수 증가) : non-causal의 성능과 비슷하거나 좋아졌습니다.
마지막으로 실제로 commited rate없이 학습을 해보니, 당연히 KL divergence가 무시할만한 수준($KL<10^{-8}\,\,bits/dim$)으로 떨어지며 posterior collapse문제를 해결할 수 없는 것도 확인했다고 합니다.
4. Text Result
위는 모두 이미지와 관련된 실험이었는데, 텍스트의 결과는 아래와 같이 “모델이 얼마나 데이터를 잘 설명하는지”를 비교한 log-likelihood면에서 다른 autoregressive모델에 비해 오히려 성능이 안좋았다고 합니다.
** 논문에는 명확히 나와 있지 않지만 NLL(KL term)값을 구한 것 같습니다.

하지만 KL term값을 보면 값이 유의미하게 존재하므로, latent variable의 사용량이 크다고 볼 수 있습니다.
https://chickencat-jjanga.tistory.com/3
https://heygeronimo.tistory.com/39
코드 : https://velog.io/@hong_journey/VAEVariational-AutoEncoder-구현하기
사진 : https://velog.io/@tobigs-gm1/Variational-Autoencoder
posterior collapse 분석 : https://datascience.stackexchange.com/questions/48962/what-is-posterior-collapse-phenomenon
