2024. 12. 4. 23:55ㆍDevelopers 공간 [SOTA]
- Paper : https://openreview.net/forum?id=LyJi5ugyJx
- Authors
- Yang Song + OpenAI, ICLR’25
- Main Idea
- 새로운 parametrization TrigFlow를 제안해 기존 discrete-time CM과 continuous-time CM 모두의 성능을 향상합니다.
- 위 formulation은 기존의 EDM, Flow Matching, V-Prediction을 통합한 개념입니다.
- 위 formulation을 통해 기존 continuous-time CM의 instability의 원인을 파악해 개선이 가능합니다.
- 이런 formulation 내에서 instability를 극복하기 위한 네트워크 구조와 Training Objective를 제안해 학습한 sCM을 보입니다.
- sCM을 scaling-up하기 위한 학습을 가능하게 하기 위한 방법을 제안합니다.
- ImageNet(512x512)으로 학습해 1.5B의 파라미터까지 scalable하고, 오직 2개의 sampling step만으로 기존 DM의 SOTA성능보다 10% 차이 밖에 안나는 성능을 보였습니다.
- Tasks : Unconditional Generation, Class-Conditional Generation
- Results : ImageNet(512x512), ImageNet(64x64), CIFAR-10
<구성>
0. Before Start...
a. EDM
b. Consistency Models
c. Flow Matching
1. Problem
2. Approach
a. TrigFlow
b. sCM
c. Scaling-Up sCM
3. Results
글효과 분류1 : 논문 내 참조 및 인용
글효과 분류2 : 폴더/파일
글효과 분류3 : 용어설명
글효과 분류4 : 글 내 참조
글효과 분류5 : 글 내 참조2
글효과 분류6 : 글 내 참조3
0. Before Start...
본 논문에 대해 다루기 전에 필요한 배경에 대해 간단히 살펴보겠습니다.
a. EDM
** [EDM, k-diffusion] Elucidating the Design Space of Diffusion-Based Generative Models (NIPS'22)
기존 score-based 논문에서는 다양한 forward SDE를 아래와 같이 정의할 수 있었습니다
** VE(Variance Exploding)와 VP(Variance Preservation)는 Forward Process SDE를 Discretization을 통해 연속된 t를 N개의 step으로 나타낼 때의 조건에 따라 구분됩니다.
$$p_{0t}(\mathbf{x}_t|x_0) = \left\{\begin{aligned}
\mathcal{N}(\mathbf{x}_t;&& \mathbf{x}_0,&\left[ \sigma(t)^{2}-\sigma(0)^{2} \right ]\mathbf{I})&&(VE\ SDE)\\
\mathcal{N}(\mathbf{x}_t;&& \mathbf{x}_0{\rm e}^{-\frac{1}{2}\int ^t_0\beta(s)ds},&\ \mathbf{I}-\mathbf{I}{\rm e}^{-\int ^t_0\beta(s)ds})&&(VP\ SDE)\\
\mathcal{N}(\mathbf{x}_t;&& \mathbf{x}_0{\rm e}^{-\frac{1}{2}\int ^t_0\beta(s)ds},&\left[1-{\rm e}^{-\int ^t_0\beta(s)ds}\right ]^2\mathbf{I})&&(sub-VP\ SDE)\\
\end{aligned}\right.$$
EDM에서는 SDE의 pdf형태 $p_{0t}(x_t|x_0)$를 아래와 같은 general form으로 나타는데, $s(t)$와 $\sigma(t)$를 활용해 표현했습니다.
** $\dot{s}$는 $s$를 미분한 함수, $\dot{\sigma}$은 $\sigma$를 미분한 함수입니다.
** 아래 pdf는 당연히 SDE식으로 표현할 수 있고, SDE 표현식의 VP, VE에 따라 다른 f(t)와 g(t)로 표현을 할 수도 있습니다.
$$\begin{aligned}
&p_{0t}(x_t|x_0)&=&\mathcal{N}(x;\mu,\Sigma)\\
&&=& \mathcal{N}(x_t;s(t)x_0, s(t)^2\sigma(t)^2I)\\
&when\ &&s(t)=exp(\int^t_0f(\xi) d\xi)\\
&&&\sigma(t)=\sqrt{\int^t_0\frac{g(\xi)^2}{s(\xi)^2}d\xi}\\
&and\ &&f(t)=\dot{s}(t)/s(t)\\
&&&g(t)= s(t)\sqrt{2\dot{\sigma}(t)\sigma(t)}
\end{aligned}$$
기존의 score-based에서는 reverse ODE를 $dx_t=[f(t)x_t-\frac{1}{2}g(t)^2\nabla _{x_t}logp_t(x_t)]dt$로 정의했었는데, 위 정의를 활용해 표현하면 아래와 같이 reverse ODE를 표현할 수 있습니다.
$$\begin{aligned}
d\boldsymbol{x} &=[f(t)x&-&\frac{1}{2}g(t)^2&\nabla_{x}logp_t(x)&]\mathrm{d} t\\
&=[f(t)x&-&\frac{1}{2}g(t)^2&\nabla_{x}logp(\frac{x}{s(t)};\sigma(t))&]\mathrm{d} t\\
&= [\frac{\dot{s}(t) }{s(t)}x&-&s(t)^{2} \dot{\sigma}(t) \sigma(t) &\nabla_{x} \log p(\frac{x}{s(t)} ; \sigma(t))&] \mathrm{d} t
\end{aligned}$$
중요한 것은 본 논문에 따르면 VE는 $\sigma(t)=t,s(t)=1$이므로, 위에서 나온 forward SDE에 따르면 VE forward SDE는 아래와 같고,
$$\boldsymbol{x}_t=\boldsymbol{x}_0+t\boldsymbol{z}_t\text{ when }\boldsymbol{z}_t\sim \mathcal{N}(\boldsymbol{0},\boldsymbol{I})$$
위에서 나온 reverse ODE에 따르면 VE reverse ODE는 아래와 같습니다.
$$\mathrm{d}\boldsymbol{x}=-t\nabla_x log\ p(\boldsymbol{x};t)\mathrm{d}t$$
위 식중 score function $\nabla_x log\ p(\boldsymbol{x};t)$는 본 논문에서 아래와 같은 Denoiser Function $D_\theta$으로 바꾸어 표현가능합니다.
Denoiser Function $D(x;\sigma)$는 "$p_{data}$로부터 얻어 낸 샘플 이미지 y에 noise n을 더한 값"인 x를 input으로 받아, noise가 제거된 이미지를 예측합니다.
$$\mathrm{d}\boldsymbol{x}=\frac{1}{t}(\boldsymbol{x}-D_\theta(x;t))\mathrm{d}t$$
그리고 Denoiser Function는 아래 식과 같이 x에서 제거될 noise를 예측하는 $F_\theta$ Network로 구성됩니다. 정확히는 n-scaled unit variance를 예측합니다.
** Denoiser Function은 $D_\theta(x,t)$, $\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)$로 표현합니다.
$$\begin{aligned}
&D_\theta(x,t)&&=x-t{\color{red}\boldsymbol{F}_\theta(}x,t{\color{red})}\\
=&\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)&&={\color{blue}c_{skip}(t)}\boldsymbol{x}_t+{\color{blue}c_{out}(t)}{\color{red}\boldsymbol{F}_\theta(}{\color{blue}c_{in}(t)}\boldsymbol{x}_t,{\color{blue}c_{noise}(t)}{\color{red})}
\end{aligned}$$
위 파란색으로 된 파라미터는 직접 디자인된 coefficents들인데, EDM에서는 이 파라미터들을 통해 training objective가 timestep과 무관하게 항상 unit variance를 가지도록 셋팅을 합니다.
$$\begin{aligned}
\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)&={\color{blue}c_{skip}(t)}\boldsymbol{x}_t+{\color{blue}c_{out}(t)}{\color{red}\boldsymbol{F}_\theta(}{\color{blue}c_{in}(t)}\boldsymbol{x}_t,{\color{blue}c_{noise}(t)}{\color{red})}\\
{\color{blue}c_{skip}(t)}&=\frac{\sigma^2_d}{(\sigma^2+\sigma^2_d)}\\
{\color{blue}c_{out}(t)}&=\frac{\sigma_d\cdot \sigma}{\sqrt{\sigma^2+\sigma^2_d}}\\
{\color{blue}c_{in}(t)}&=\frac{1}{\sqrt{\sigma^2+\sigma^2_d}}\\
{\color{blue}c_{noise}(t)}&=\frac{1}{4}ln(\sigma)\\
\sigma(t)&=t
\end{aligned}$$
Denoiser Function이 학습되면, 위에 나왔던 reverse VE ODE, 즉 VE PF(Probability Flow) ODE를 활용해 $\boldsymbol{x}_T\sim\mathcal{N}(\boldsymbol{0},T^2\boldsymbol{I})$에서부터 $\boldsymbol{x}_0$까지 나아갑니다.
$$\mathrm{d}\boldsymbol{x}=\frac{1}{t}(\boldsymbol{x}-D_\theta(x;t))\mathrm{d}t$$
b. Consistency Models
** [CM] Consistency Models (arxiv'23)
기존의 DM은 이미지, 오디오, 비디오 등을 생성하기 위해 발전되었지만, iterative한 sampling process를 거치기 때문에 느린 generation과정이 문제가 됩니다.
이를 극복한 빠른 sampling을 위해 아래와 같은 방법들이 제안되었습니다.
- ODE Solvers : 10 step이 필요합니다.
** DDIM, DEIS, DPM-solver, GENIE - Distillation Techniques : single step이 가능한 것도 있지만, DM으로부터 많은 샘플 데이터를 추출해야하기 때문에 이 또한 computationally expensive하다고 합니다.
** Knowledge distillation in iterative generative models for improved sampling speed (arxiv’21)
** Progressive distillation for fast sampling of diffusion models (arxiv’22) **
** On distillation of guided diffusion models (cvpr’23)
** Fast sampling of diffusion models via operator learning (ICML’23)
위와 같은 기법들이 가진 문제점들을 극복하기 위해 높은 퀄리티이면서도 직접적으로 one-step을 통해 noise를 data로 mapping하는 consistency models를 소개합니다.
** 물론 여전히 multi-step도 가능하고, computation과 sample quality 간의 trade-off가 존재합니다.

이미 존재하는 DM distillation 방법보다 높은 성능을 보였으며, one-step 생성에 있어서 SOTA결과를 보였습니다.
먼저 복습을 해보겠습니다. score-based 논문에서 제안된 SDE와 ODE는 아래와 같은 형태를 가집니다.
** score model $\boldsymbol{s}_\phi(\boldsymbol{x},t)\approx \nabla log p_t(\boldsymbol{x}_t)$
$$\begin{aligned}
\mathrm{d}\boldsymbol{x}_t&=\boldsymbol{\mu}(\boldsymbol{x}_t, t)\mathrm{d}t+\sigma(t)\mathrm{d}\boldsymbol{w}_t&\text{SDE forward}\\
\mathrm{d}\boldsymbol{x}_t&=\left[\boldsymbol{\mu}(\boldsymbol{x}_t,t)-\frac{1}{2}\sigma(t)^2{\color{red}\nabla log p_t(\boldsymbol{x}_t)}\right]\mathrm{d}t&\text{PF ODE solution}
\end{aligned}$$
용어는 아래와 같습니다.
- $p_{data}(x)=p_0(x)$ : data distribution
- $p_t(x)=x_t \text{distribution}$ : noisy image distribution
- $p_T\sim \pi(x)\approx \mathcal{N}(0,t^2\boldsymbol{I})$ : noise distribution (~tractable Gaussian Distribution)
먼저, 본 논문에서는 EDM 논문의 셋팅을 따라 아래와 같이 셋팅합니다.
** 기존 EDM 논문에서는 $\sigma(t)=t, s(t)=1$ 이므로 $\mathrm{d}x=-t\nabla log p_t(\boldsymbol{x}_t)\mathrm{d}t$이고 이를 VE(Variance Exploding) ODE라고 합니다.
$$\begin{matrix}
\boldsymbol{\mu}(\boldsymbol{x}_t, t)&=0\\
\sigma(t)&=\sqrt{2t}
\end{matrix}$$
또한 EDM과 같이 boundary와 discrete-timestep schedule은 아래와 같이 하며, N이 충분히 클 때 $\rho=7$로 합니다.
$$\begin{aligned}
t_1=\epsilon<t_2<\dots<t_N=T\\
t_i=(\epsilon^{1/\rho}+{(i-1)}/{(N-1)(T^{1/\rho}-\epsilon^{1/\rho})})^\rho
\end{aligned}$$
위 셋팅으로 인해 t step에서의 분포에 대해 solution trajectory는 아래와 같이 정리됩니다. 이를 CM논문에서는 empirical PF ODE라고 합니다.
$$\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}=-t\boldsymbol{s}_\phi (\boldsymbol{x}_t,t)$$
sampling 과정은 $\hat{\boldsymbol{x}}_T\sim\pi=\mathcal{N}(\boldsymbol{0}, T^2\boldsymbol{I})$에서 추출된 초기 노이즈를 가지고 numerical ODE(Euler, Heun solvers)를 활용해 trajectory $\{\hat{\boldsymbol{x}}_t\}t\in [0,T]$를 따라 $\hat{\boldsymbol{x}}_0$를 향해 진행됩니다.
이렇게 얻은 $\hat{\boldsymbol{x}}_0$, 즉 approximate sample의 분포는 위에서 정의한 $p_{data}(x)$와 비슷한 결과일 것으로 기대될 것입니다.
또한 EDM에서는 numerical instability때문에 $t=\epsilon$에서 멈추고 이$\hat{\boldsymbol{\epsilon}}$를 approximate sample로 활용하기도 했습니다.
이와 비슷하게 CM논문에서는 이미지 pixel을 [-1,1]로 rescale했으며, T=80, $\epsilon$=0.002로 만들어주었습니다.
CM논문에서 제안하는 Consistency Model은 아래 두가지의 방법으로 학습이 가능합니다.
- Distillation Mode : pre-trained DM의 지식을 single-step sampler로 옮기는 방식으로, 기존 disillation 방식보다 퀄리티가 좋았다고 합니다.
- Isolation Mode : 독립적으로 학습되는 방식입니다.
다음으로 CM논문에서는 Consistency 함수 $\boldsymbol{f}$이라는 것을 먼저 정의합니다.
$$\boldsymbol{f}:(\boldsymbol{x}_t,t)\rightarrow \boldsymbol{x}_\epsilon$$
이 함수는 self-consistency라는 특징을 가지고 있다고 하는데, 이 말인 즉 "임의의 PF ODE trajectory에 포함되는 $(\boldsymbol{x}_t,t)$쌍에 대한 consistency 함수의 output은 consistent하다"는 뜻입니다.
$$\begin{aligned}
\boldsymbol{f}(\boldsymbol{x}_t,t)&=\boldsymbol{f}(\boldsymbol{x}_{t'},t')&&\text{ for all }t,t'\in [\epsilon, T]&\\
\boldsymbol{f}(\boldsymbol{x}_\epsilon,t)&=\boldsymbol{x}_\epsilon &&\text{ when }\boldsymbol{f}()\text{ is identity function}&\text{ ( boundary condition )}
\end{aligned}$$
우리의 목적은 아래 그림과 같이 $\boldsymbol{f}_\theta$라는 self-consistency라는 특징을 가지는 Consistency 모델을 학습하는 것입니다.
** 이는 neural flows와 비슷하기도 하지만, invertible하도록 강제하지는 않습니다.

위 consistency 모델의 Boundary Condition은 $F_\theta(\boldsymbol{x},t)$라는 DNN이 있을 때, 아래와 같은 두가지 방법으로 구현이 가능합니다.
** $F_\theta(\boldsymbol{x},t)$의 output은 $\boldsymbol{x}$과 같은 차원을 가집니다.
- 간단한 방법 : $f_\theta(\boldsymbol{x}_\epsilon, \epsilon)=\left\{\begin{aligned}
&\boldsymbol{x}&\ &t=\epsilon\\
&F_\theta(\boldsymbol{x},t)&\ &t\in(\epsilon,T]
\end{aligned}\right.$ - skip connection을 활용 : $f_\theta(\boldsymbol{x}_\epsilon, \epsilon)=c_{skip}(t)\boldsymbol{x}+c_{out}(t)F_\theta(\boldsymbol{x},t)$
** $c_{skip}(t)$ 와 $c_{out}(t)$는 미분 가능한 함수 이며, $c_{skip}(\epsilon)=1$ 와 $c_{out}(\epsilon)=0$입니다.
이 중에 2. skip connection을 활용하면 Consistency 모델이 $t=\epsilon$에서 미분가능해서 continuous-time의 consistency model을 학습 가능해지기 때문에, 2번 방법을 활용합니다. 이는 결국 EDM의 수식과 굉장히 비슷한 모습을 가지고 있습니다.
** 하지만 EDM에서의 수식이었던 $\mathrm{d}\boldsymbol{x}=\frac{1}{t}(\boldsymbol{x}-\boldsymbol{f}_\theta(x;t))\mathrm{d}t$ 수식 중 $\boldsymbol{f}_\theta(x;t)$만 사용하는 것은 "노이즈가 제거된 이미지 자체"를 바로 만들어내는 것이 Consistency모델의 목적이지, 그 gradient를 구하는것이 목적은 아니기 때문이겠죠.
그럼 모델의 Sampling과 학습이 어떻게 진행되는지 살펴보겠습니다.
1. Sampling
Consistency 모델 $\boldsymbol{f}_\theta$를 잘 학습한 뒤에, 샘플링하는 과정은 아래와 같습니다.
- Step1. $\hat{\boldsymbol{x}}_T\sim\pi=\mathcal{N}(\boldsymbol{0}, T^2\boldsymbol{I})$에서 초기 노이즈를 얻은 뒤에
- Step2. $\hat{\boldsymbol{x}}_\epsilon=\boldsymbol{f}_\theta(\hat{\boldsymbol{x}}_T, T)$ 모델을 통해 바로 최종 샘플을 얻습니다.
- Step+. 여러번 반복할 때는 timestep을 적용하는 형태가 아닌 Step1과 Step2를 반복하는 형태로 진행하며, 반복하고 싶은 timestep $\{\tau_1,\tau_2,\tau_3,\dots \tau_{N-1}\}$는 greedy algorithm을 통해 찾습니다.
즉, FID를 최적화하는 포인트를 ternary search를 통해 찾습니다.

이에 추가적으로 DM과 마찬가지로 Zero-shot data editing을 위해서는, 따로 학습은 하지 않고 latent space 에서의 interpolation을 통해 진행합니다.
** Zero-shot data editing : image editing-inpainting, colorization, super-resolution, stroke-guided image editing
** 앞서 정의한 바와 같이 Consistency model은 $\boldsymbol{x}_\epsilon\leftarrow \boldsymbol{x}_t$이므로 latent space는 $t\in [\epsilon,T]$에서 진행되며, 위 Step+와 같은 여러번 반복해 진행합니다.
2. Distillation Mode : Consistency Distillation (CD)
pre-trained score 모델 $\boldsymbol{s}_\phi (\boldsymbol{x},t)$을 distill 함으로써 Consistency model을 학습하는 방법을 소개하겠습니다.
- Step1. $\boldsymbol{x}_{t_{n+1}}$ 만들기
- 데이터 분포에서 샘플 $\boldsymbol{x}\sim p_{data}(\boldsymbol{x})$을 샘플링 한 뒤,
gaussian noise를 SDE $\mathcal{N}(\boldsymbol{x},t^2_{n+1}\boldsymbol{I})$를 통해 더하고 $\boldsymbol{x}_{t_{n+1}}$를 만들어 줍니다.
- 데이터 분포에서 샘플 $\boldsymbol{x}\sim p_{data}(\boldsymbol{x})$을 샘플링 한 뒤,
- Step2. $(\hat{\boldsymbol{x}}_{t_n}^\phi,\boldsymbol{x}_{t_{n+1}})$ 포인트 쌍 만들기
- 위 $\boldsymbol{x}_{t_{n+1}}$에서 pre-trained score 모델 $\boldsymbol{s}_\phi (\boldsymbol{x},t)$을 활용해 $\hat{\boldsymbol{x}}_{t_n}^\phi$를 만들어줍니다.
- 그 과정은 아래와 같습니다.
- pre-trained score 모델 $\boldsymbol{s}_\phi (\boldsymbol{x},t)$가 있을 때, 아래와 같은 N-1개의 sub interval이 있는 N개의 discritized time step들이 있다고 하겠습니다.
$$\epsilon=t_1<t_2<\dots<t_N=T$$ - N이 굉장히 클때, numerical ODE solver를 활용해 하나의 discretized step간의 이동은 아래와 같습니다.
** $\Phi(\dots, ;\phi)$는 $\phi$에 대해 Euler solver와 같은 one-step ODE solver를 활용한 update 함수입니다. 앞서 정의한 empirical PF ODE의 경우 아래와 빨간색 부분과 같이 적용됩니다.
$$\begin{aligned}
\hat{\boldsymbol{x}}^\phi_{t_n}&:=\boldsymbol{x}_{t_{n+1}}+(t_n-t_{n+1})\Phi(\boldsymbol{x}_{t_{n+1}}, t_{n+1};\phi)\\
&=\boldsymbol{x}_{t_{n+1}}+(t_n-t_{n+1}){\color{red}t_{n+1}\boldsymbol{s}_\phi (\boldsymbol{x}_{t_{n+1}},t_{n+1})}
\end{aligned}$$
- pre-trained score 모델 $\boldsymbol{s}_\phi (\boldsymbol{x},t)$가 있을 때, 아래와 같은 N-1개의 sub interval이 있는 N개의 discritized time step들이 있다고 하겠습니다.
- 그래서 결국엔 Step1, Step2를 통해 $(\hat{\boldsymbol{x}}_{t_n}^\phi,\boldsymbol{x}_{t_{n+1}})$라는 인접한 데이터 포인트 쌍이 구해질 것입니다.
- Step3. Loss적용하기
- 앞서 구해진 $(\hat{\boldsymbol{x}}_{t_n}^\phi,\boldsymbol{x}_{t_{n+1}})$라는 인접한 데이터 포인트 쌍에 대해 Consistency 모델 output의 차이를 최소화하도록 consistency 모델을 학습합니다.
- 이 때 사용하는 Consistency Distillation Loss는 아래와 같습니다.
** $\lambda(\cdot )$은 weighting함수이며, $\lambda(t_n)\equiv 1$일 때 모든 task와 데이터셋에서 잘 동작했다고 합니다.
** $d(\cdot,\cdot)$은 Distance-metric function이며, 본 논문에서는 squared $l_2$ distance, $l_1$ distance, LPIPS을 활용했습니다.
$$\begin{aligned}
\mathcal{L}_{CD}^N({\color{red}\theta^-},{\color{blue}\theta};\phi)&:=\mathbb{E}[\lambda(t_n)d({\color{red}\boldsymbol{f}_{\theta^-}(\hat{\boldsymbol{x}}^\phi_{t_{n}}, t_{n})}, {\color{blue}\boldsymbol{f}_\theta(\boldsymbol{x}_{t_{n+1}}, t_{n+1})})]&\\
{\color{red}\theta^-}&=stopgrad(\mu\theta^-+(1-\mu)\theta)&\text{EMA when }0\leq\mu<1
\end{aligned}$$
위에서의 $\boldsymbol{f}_\theta$를 Online network라고 부르며, $\boldsymbol{f}_{\theta^-}$를 Target network라고 부릅니다.
결과적으로 위 알고리즘은 아래와 같이 정리됩니다.

3. Isolation Mode : Consistency Training (CT)
이번엔 pre-trained DM에 의존하지 않고 학습하는 방법을 보이겠습니다. 이를 통해 distillation 기술과 다르게 CM을 독립적으로 구축할 수 있습니다.
- Step1. $\boldsymbol{x}_{t}$ 만들기
- 데이터 분포에서 샘플 $\boldsymbol{x}\sim p_{data}(\boldsymbol{x})$을 샘플링하고,
gaussian noise를 SDE $\mathcal{N}(\boldsymbol{x},t^2\boldsymbol{I})$를 통해 더하고 $\boldsymbol{x}_{t}$를 만들어 줍니다.
- 데이터 분포에서 샘플 $\boldsymbol{x}\sim p_{data}(\boldsymbol{x})$을 샘플링하고,
- Step2. $({\boldsymbol{x}}_{t_n},\boldsymbol{x}_{t_{n+1}})$ 포인트 쌍 만들기
- 이때, 기존에는 pre-trained score 모델 $\boldsymbol{s}_\phi (\boldsymbol{x},t)$를 통해 구해주었던 score 함수 $\nabla log p_t(\boldsymbol{x}_t)$를 이번엔 아래와 같은 unbiased estimator를 통해 구해냅니다.
$$\begin{aligned}
\nabla log p_t(\boldsymbol{x}_t)&=\nabla_{\boldsymbol{x}_t}log\int p_{data}(\boldsymbol{x})p(\boldsymbol{x}_t|\boldsymbol{x})\mathrm{d}x\\
&=\int p(\boldsymbol{x}|\boldsymbol{x}_t)\nabla_{\boldsymbol{x}_t}log p(\boldsymbol{x}_t|\boldsymbol{x})\mathrm{d}x\\
&=\mathbb{E}(\nabla_{\boldsymbol{x}_t}log p(\boldsymbol{x}_t|\boldsymbol{x})|\boldsymbol{x}_t)\\
&=-\mathbb{E}\left[\frac{\boldsymbol{x}_t-\boldsymbol{x}}{t^2}|\boldsymbol{x}_t\right]
\end{aligned}$$- 즉, score function의 estimate를, $N\rightarrow \infty$일 때 Euler ODE solver $\frac{\boldsymbol{x}_t-\boldsymbol{x}}{t^2}$의 몬테카를로 샘플링 평균값으로 estimate값으로 추정할 수 있다는 말입니다.
- 하지만 실제로는 $N\rightarrow \infty$가 아니기 때문에 numerical error는 발생할 수 밖에 없겠죠
- 위와 같은 unbiased estimator를 활용해 인접한 샘플 쌍 $({\boldsymbol{x}}_{t_n},\boldsymbol{x}_{t_{n+1}})$을 구합니다. 어렵게 설명했지만 결국에는 정의했던 diffusion SDE에 의한 인접한 샘플 쌍을 할용해 Loss를 Step3와 같이 구할 수 있습니다.
- 이때, 기존에는 pre-trained score 모델 $\boldsymbol{s}_\phi (\boldsymbol{x},t)$를 통해 구해주었던 score 함수 $\nabla log p_t(\boldsymbol{x}_t)$를 이번엔 아래와 같은 unbiased estimator를 통해 구해냅니다.
- Step3. Loss 적용하기
- 위 상황에서 아래와 같은 몇가지 조건을 만족하는 경우, 위와 같이 score function을 estimation하면 CM 논문에 언급된 Theorem 2를 통해 아래와 같은 CT(Consistency Training) Loss를 통해 학습이 가능하다고 합니다.
- 조건1. $\Delta t :=max_{n\in [[1,N-1]]}\{\|t_{n+1}-t_n\|\}$
- 조건2. $\mathrm{d}$와 $\boldsymbol{f}_{\theta^-}$가 모두 두번 미분 가능
- 조건3. $\lambda()$는 bounded
- 조건4. 기대값 $\|\nabla log\ p_{t_n}(\boldsymbol{x}_{t_n})\|^2_2< \infty$
- 조건5. Euler ODE solver를 활용할 계획
- 조건6. pretrained score model $\boldsymbol{s}_\phi (\boldsymbol{x},t)$과 Ground Truth $\nabla log p_t(\boldsymbol{x}_t)$가 일치 할때
- CT(Consistency Training) Loss는 아래와 같습니다.
$$\begin{aligned}
\mathcal{L}^N_{CD}(\theta, \theta^-;\phi)&=\mathcal{L}^N_{CT}(\theta, \theta^-)+o(\Delta t)\\
\mathcal{L}^N_{CT}(\theta, \theta^-)&=\mathbb{E}[\lambda(t_n)d({\boldsymbol{f}_\theta({\color{red}\boldsymbol{x}+t_{n+1}\boldsymbol{z}}, t_{n+1})},{\boldsymbol{f}_{\theta^-}({\color{red}\boldsymbol{x}+t_n\boldsymbol{z}}, t_n)})]
\end{aligned}$$
- 위 상황에서 아래와 같은 몇가지 조건을 만족하는 경우, 위와 같이 score function을 estimation하면 CM 논문에 언급된 Theorem 2를 통해 아래와 같은 CT(Consistency Training) Loss를 통해 학습이 가능하다고 합니다.
- Step4. 학습 중 적절하게 schedule하기
- 추가적으로 progressively하게 증가하는 N을 만드는 schedule function $N()$을 학습에 활용하는 것이 더욱 성능이 향상된다고 합니다.
- 아래의 그림을 보면
- N이 적을 때, 아래 식의 CD Loss에 대한 높은 bias와 적은 variance를 가지며, 이는 학습 초반의 빠른 convergence를 도울 것입니다.
- N이 클 때, 아래 식의 CD Loss에 대한 낮은 bias와 높은 variance를 가지며, 이는 학습 후반에 성능을 향상시키기 위해 유리할 것 입니다.
$$\mathcal{L}^N_{CT}(\theta, \theta^-)={\color{red}\mathcal{L}^N_{CD}(\theta, \theta^-;\phi)}-o(\Delta t)$$
- 추가적으로 본 논문에서는 이 schedule function $N()$에 따라서 EMA 모델을 학습하는 decay rate $\mu()$ 또한 변화해야한다고 합니다.

결과적으로 위 알고리즘은 아래와 같이 정리됩니다.

<Continuous-time CM>
마지막으로 본 논문에서는 CD와 CT학습에 대해 적절한 condition내에서 $N\rightarrow \infty(\Delta t\rightarrow 0)$일 때, 즉 infinite한 timestep 개수로 일반화해 Continuous-time으로까지 확장하는 내용이 Appendix B에 추가되어있습니다.
간단히 보이면 loss의 gradient는 $d()$ metric 함수를 squared $l_2$ distance를 활용했을 때의 gradient는 아래와 같습니다.
$$\begin{aligned}
&\nabla_\theta\mathbb{E}_{\boldsymbol{x}_t,t}[w(t)\boldsymbol{f}_\theta^\top(\boldsymbol{x}_t,t){\color{red}\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}]&\\
{\color{red}\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}&=\nabla_{\boldsymbol{x}_t}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}+\delta_t\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)&\text{ (tangent of }\boldsymbol{f}_{\theta^-}\text{ at }(\boldsymbol{x}_t,t)\text{)}
\end{aligned}$$
Continuous-time CM이 되면, N이라는 특정 timestep이 없어지지만 미분 함수와 Jacobian vector 곱을 통해 구현됩니다.
** Jacobian Matrix : 도함수 행렬
근데, 이는 사실 딥러닝 프레임워크에서 잘 지원되지는 않으며, 실제로는 continuous-time CM은 굉장히 최적화가 굉장히 instable하다고 합니다.
그리고 사실 discrete-time CM에서도 너무 작은 $\Delta t$에서는 같은 결과가 나오기도 합니다.
<다른 CM에서의 개선>
또한 이후에 다른 논문 에서는 Discrete CM을 개선하기 위해 다양한 시도를 했습니다. 어떤 것들이 있었는지 간단히 살펴보겠습니다.
** Improved techniques for training consistency models (arxiv’23)
** Consistency models made easy (arxiv’24)
위에서 표현한 Discrete한 CM의 training objective를 일반화해 표현하면, 두개의 인접한 timestep에서의 distance는 아래와 같습니다.
$$\mathbb{E}_{\boldsymbol{x}_t,t}[w(t){\color{red}d(}{\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)},{\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_{t-{\color{blue}\Delta t}},t-{\color{blue}\Delta t})}{\color{red})}]$$
이후에 다른 논문에서는 위 $d()$라는 metric 함수를 squared $l_2$ distance, $l_1$ distance, LPIPS가 아닌 Pseudo-Huber loss $d(\boldsymbol{x},\boldsymbol{y})=\sqrt{\|\boldsymbol{x}-\boldsymbol{y}\|^2_2+c^2}-c\text{ when } c>0$을 활용하거나 LPIPS loss를 활용했으며,
또한 위와 같은 discrete-time CM이 $\Delta t$의 선택에 민감하므로, 이후의 두 논문에서는 빠른 convergence를 위해 이 $\Delta t$를 직접 디자인된 annealing schedule을 통한 값을 활용했습니다.
** 하지만 역시나 이런 방법들은 여전히 PF-ODE와 numerical ODE solver를 활용하므로 step size $\Delta t$에 의한 discretization error가 발생합니다.
c. Flow Matching
** Non-Denoising Forward-Time Diffusions (arxiv’23)
** Flow matching for generative modeling (arxiv’22)
** [Rectified Flow] Flow Straight And Fast : Learning to generate and transfer data with Rectified Flow(arxiv'22)
** Stochastic interpolants: A unifying framework for flows and diffusions (arxiv’23)
** Iterative α-(de) blending: A minimalist deterministic diffusion model (SIGGRAPH’23)
Flow Matching(Stochastic Interpolants, Rectified Flow)의 정의는 $p_1(x)$가 gaussian 분포이고, $p_0(x)$가 data 분포일 때, $X_1$에서 $X_0$으로 이동하는 ODE를 Drift Force(velocity) $v$로 표현해 학습하는 방법입니다.
** 보통 Flow matching 논문에서는 $p_0(x)$는 gaussian 분포이고, $p_1(x)$이 data 분포입니다. 필자가 임의로 헷갈릴까봐 바꿔 표현했습니다.
$$\begin{aligned}
\mathrm{d}Z_t&=v(Z_t,t)dt\\
&\underset{v}{min}\int^1_0\mathbb{E}[\left\| (X_0-X_1)-v(X_t,t)\right\|^2]\mathrm{d}t
\end{aligned}$$
조금 더 자세히 살펴보겠습니다. conditional distribution이 아래와 같을 때, 각 평균과 분산을 아래와 같이 정의하면 이동한 값을 정의할 수 있습니다.
$$\begin{aligned}
p_t(\boldsymbol{x}|x_0)&=\mathcal{N}(\boldsymbol{x}|\mu_t(x_0),\sigma_t(x_0)^2\boldsymbol{I})\\
\mu_t(\boldsymbol{x})&=tx_0\\
\sigma_t(x)&=1-t\\
v_t(\boldsymbol{x}|x_0)&=\frac{x_0-\boldsymbol{x}}{1-t}
\end{aligned}$$
혹은 식으로 나타내면 아래와 같습니다.
$$\begin{aligned}
\boldsymbol{x}_t&=\alpha_t\boldsymbol{x}_0+\sigma_t\boldsymbol{z}\\
\alpha_t&=1-t\\
\sigma_t&=t\\
\boldsymbol{v}_t&=\frac{\mathrm{d}\alpha_t}{\mathrm{d}t}\boldsymbol{x}_0+\frac{\mathrm{d}\sigma_t}{\mathrm{d}t}\boldsymbol{z}
\end{aligned}$$
이런 상황에서 Loss를 활용해 네트워크 $\boldsymbol{F}_\theta$ 혹은 $\boldsymbol{v}_\theta$를 학습하는 코드는 아래와 같습니다.
$$\begin{aligned}
\underset{\theta}{min}\mathbb{E}&\left\|\boldsymbol{F}_\theta(x,t)-v_t(x|x_0)\right\|^2\\
&\left\|\boldsymbol{F}_\theta(x,t)-\frac{x_0-x}{1-t}\right\|^2
\end{aligned}$$
이제 아래와 같은 식을 활용한 PF-ODE를 활용해 $\boldsymbol{x}_1\sim\mathcal{N}(\boldsymbol{0},\boldsymbol{I})$, 즉 t=1에서부터 t=0으로 진행됩니다.
$$\mathrm{d}\boldsymbol{x}=\boldsymbol{F}_\theta(\boldsymbol{x}_t,t)\mathrm{d}t$$
이후 Rectified Flow논문에서는 이외에도 flow의 crossing한 부분을 줄이기 위해 rewire하거나,

transport cost를 줄이기 위해 straight하게 학습하도록 하는 reflow방법을 추가해 step 수를 줄일 수 있음을 보였으며,

더 나아가 k-th rectified flow $Z^k$를 distillation을 통해 더 단축시킬 수 있음을 보였습니다.
Rectified Flow 알고리즘은 아래와 같이 정리할 수 있습니다.

1. Problem
기존의 CM은 pre-trained DM의 필요성없이 CT학습을 통해 구축이 가능하다는 것을 보이고, 적은 step만으로 생성이 가능해 빠른 sampling을 위해 최적화된 DM이이었습니다.
하지만 기존의 CM들은 EDM에서 정의한 VE-ODE에 의해 score function을 정의하므로 discretized timestep을 활용해 학습합니다.
이 때문에 timestep을 굉장히 조심히 scheduling 해야하며, 그렇지 못하면 discretization error를 발생해 sub-optimal인 샘플 퀄리티를 얻을 수밖에 없습니다.
따라서 continuous-time formulation을 활용하면 이런 단점들이 줄어들 수 있습니다.
아래 그림을 보면 Discrete-time CM은 numerical ODE solver를 활용하기 때문에 discretization error가 $O(\Delta t)$만큼 발생하지만, Continuous-time CM은 ODE trajectory 상에서 유지되기 때문에 앞과 다르게 학습과정에서의 부정확한 prediction을 하지 않습니다.
- 그림 중 top & middle : Discrete-time CMs
- 그림 중 bottom : Continuous-time CMs
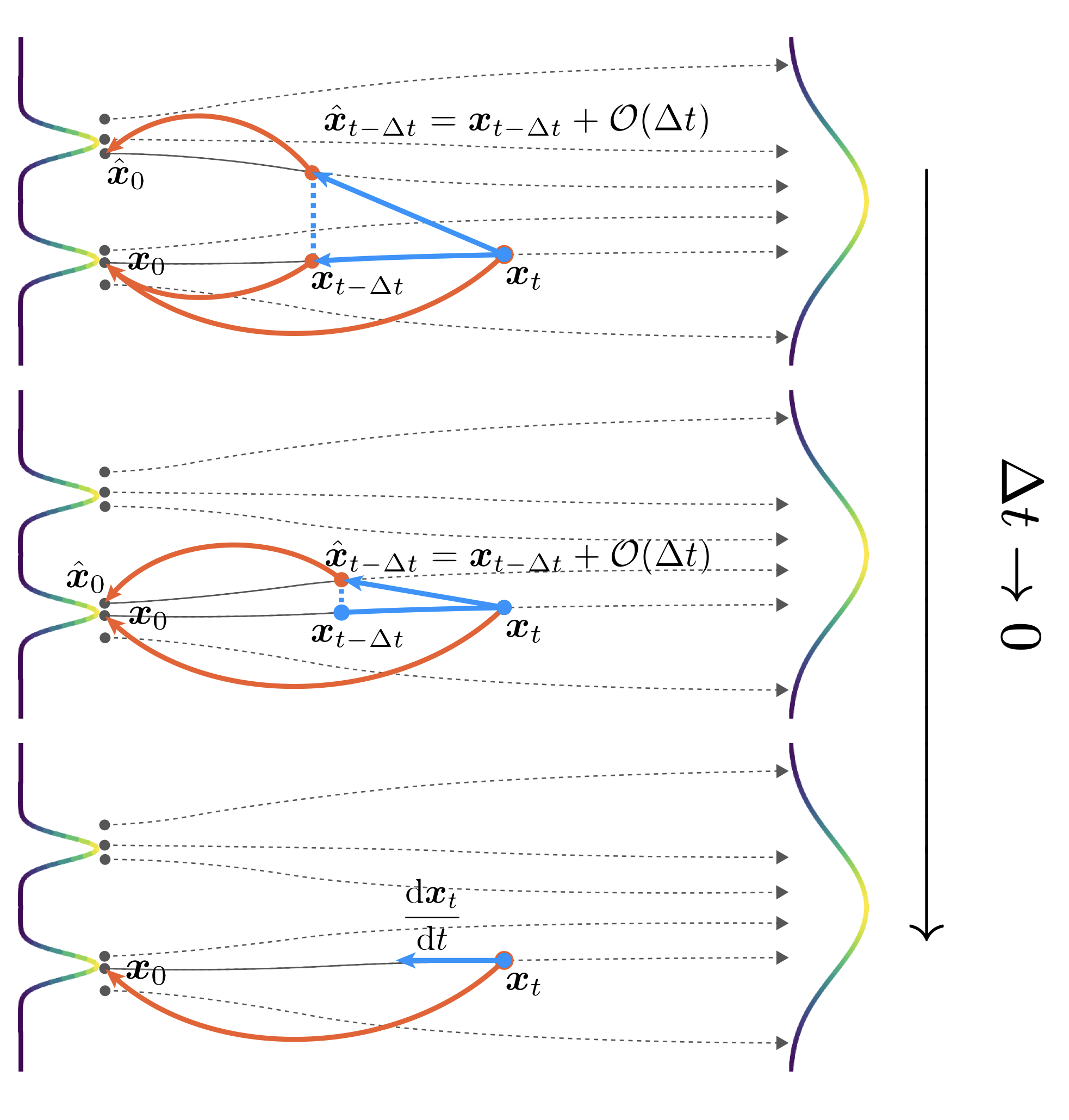
하지만 continuous-time CM은 학습할 때의 instability 때문에 보통은 제한적이었습니다.
따라서 본 논문에서는 continous-time CM 학습을 scale up이 가능할 정도로, 안정화하고 단순화하기 위한 simplified된 프레임워크이자 formulation인 TrigFlow를 제안합니다.
그리고 이런 formulation을 바탕으로, 앞서 언급한 CM학습의 instability의 근본적인 원인을 파악하고, 이에 대한 해결책으로 개선된 네트워크 구조와 training objective까지도 제안합니다.
- 네트워크 구조 : 향상된 time-conditioning과 Adaptive Group-Normalization
- Training Objective : 아래의 기법들을 활용해 continuous-time CM의 training objective를 re-formulation합니다.
- 가장 중요한 key term을 Adaptive weighting & Normalization
- 안정적이고 scalable한 학습을 위한 progressive annealing
이를 활용해 학습한 모델을 sCM이라고 부르며, 아래 그림은 ImageNet(512x512)에서 학습한 다양한 모델의 Sample Quality(FID)와 Effective Sampling Compute입니다.
** Effective Sampling Compute : (1 billion parameter) x (sampling시의 function evaluation 수)

sCM은 오직 2개의 sampling step을 활용했으므로 effective sampling compute도 낮지만, 기존 DM의 SOTA성능과 10%차이밖에 안 날정도로 높은 퀄리티를 보입니다.
추가적으로 앞서 scalable도 고려했으므로, 1.5B 파라미터까지 scalable했다고 합니다.
2. Approach
그럼 어떻게 구현되었는지 살펴보겠습니다.
a. TrigFlow
먼저, 본 논문에서 제안하는 Formulation이자 Framework인 TrigFlow를 살펴보겠습니다.
복습 겸 용어를 살펴보겠습니다.
- $\sigma_d$ : 데이터 분포 $p_d$의 표준편차
- $\boldsymbol{x}_t=\alpha_t\boldsymbol{x}_0+\sigma_t\boldsymbol{z}$ : 일반적으로 $\boldsymbol{x}_0\sim p_d$와 $t\in[0,T]$에 대해 $\boldsymbol{z}\sim\mathcal{N}(\boldsymbol{0},\sigma^2_d\boldsymbol{I})$를 활용해 진행하는 forward diffusion process의 수식
- 이 때, 위 식의 $\alpha_t>0,\sigma_t>0$ 둘을 스케줄링 하는 것을 noise schedule이라고 하는데, 기존에 VDM에서는 $\alpha_t/\sigma_t$, 즉 SNR이 t가 증가함에 따라 단조롭게 감소하는 형태의 scheduling을 취합니다.
** t가 증가함은 Gaussian Noise에서 Image로 향하는 것을 의미하며 $t=0.0\rightarrow 1.0$입니다.
- 이 때, 위 식의 $\alpha_t>0,\sigma_t>0$ 둘을 스케줄링 하는 것을 noise schedule이라고 하는데, 기존에 VDM에서는 $\alpha_t/\sigma_t$, 즉 SNR이 t가 증가함에 따라 단조롭게 감소하는 형태의 scheduling을 취합니다.
- 일반적으로 DM을 학습하기 위한 Loss는 아래와 같으며, 결국에 $\boldsymbol{D}_\theta$를 학습하는 것이 중요합니다. 또한 이 $\boldsymbol{D}_\theta$는 Parametrization에 따라 어떤 것을 예측하는지 다르게 정의됩니다.
$$\mathcal{L}_{Diff}(\theta)=\mathbb{E}_{\boldsymbol{x}_0,\boldsymbol{z},t}[w(t)\|\boldsymbol{D}_\theta(\boldsymbol{x}_t,t)-\boldsymbol{x}_0\|^2_2]$$- Score function : score function을 예측하는
** score-based (ICLR'21), EBM(NIPS'19) - Noise prediction model
** score-based (ICLR'21), EBM(NIPS'19), DDPM(ICLR'22) - Data prediction model
** DDPM(ICLR'22), VDM(NIPS'21), v-prediction(ICLR'22) - Velocity prediction model
** v-prediction(ICLR'22) - EDM
** EDM(arxiv'22) - Flow Matching
- Score function : score function을 예측하는
또한 EDM에서는 Reverse에서 노이즈가 제거된 이미지를 예측하는 $\boldsymbol{D}_\theta$를, noise를 예측하는 네트워크 $\boldsymbol{F}_\theta$를 활용해 아래와 같이 parametrization을 했었습니다.
$$\begin{aligned}
&D_\theta(x,t)&&=x-t{\color{red}\boldsymbol{F}_\theta(}x,t{\color{red})}\\
=&\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)&&={\color{blue}c_{skip}(t)}\boldsymbol{x}_t+{\color{blue}c_{out}(t)}{\color{red}\boldsymbol{F}_\theta(}{\color{blue}c_{in}(t)}\boldsymbol{x}_t,{\color{blue}c_{noise}(t)}{\color{red})}
\end{aligned}$$
위 파란색으로 된 파라미터는 직접 디자인된 coefficents들인데, EDM에서는 이 파라미터들을 통해 training objective가 timestep과 무관하게 항상 unit variance를 가지도록 셋팅을 합니다.
$$\begin{aligned}
\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)&={\color{blue}c_{skip}(t)}\boldsymbol{x}_t+{\color{blue}c_{out}(t)}{\color{red}\boldsymbol{F}_\theta(}{\color{blue}c_{in}(t)}\boldsymbol{x}_t,{\color{blue}c_{noise}(t)}{\color{red})}\\
{\color{blue}c_{skip}(t)}&=\frac{\sigma^2_d}{(t^2+\sigma^2_d)}\\
{\color{blue}c_{out}(t)}&=\frac{\sigma_d\cdot t}{\sqrt{t^2+\sigma^2_d}}\\
{\color{blue}c_{in}(t)}&=\frac{1}{\sqrt{t^2+\sigma^2_d}}\\
{\color{blue}c_{noise}(t)}&=\frac{1}{4}ln(t)
\end{aligned}$$
위 EDM parametrization은 VE ODE를 활용하며 $\sigma(t)=t, s(t)=1$했을 때의 값인데, 본 논문에서는 아래와 같이 EDM을 general한 parametrization으로 나타낼 수 있다고 합니다.
이 또한 "$\boldsymbol{F}_\theta$의 input과 output이 unit variance를 갖도록" 맞춰준 방법입니다.
** 아래에서 ${\color{blue}c_{out}(t)}$는 본 논문에서 - 값만 다룹니다.
$$\begin{aligned}
\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)&={\color{blue}c_{skip}(t)}\boldsymbol{x}_t+{\color{blue}c_{out}(t)}{\color{red}\boldsymbol{F}_\theta(}{\color{blue}c_{in}(t)}\boldsymbol{x}_t,{\color{blue}c_{noise}(t)}{\color{red})}\\
{\color{blue}c_{skip}(t)}&=\frac{\sigma_t}{\alpha^2_t+\sigma^2_t}\\
{\color{blue}c_{out}(t)}&=\pm \frac{\sigma_d\alpha_t}{\sqrt{\alpha^2_t+\sigma^2_t}}\\
{\color{blue}c_{in}(t)}&=\frac{1}{\sigma_d\sqrt{\alpha^2_t+\sigma^2_t}}\\
{\color{blue}c_{noise}(t)}&=?
\end{aligned}$$
본 논문에서는 이렇게 unit variance를 가지도록 셋팅하는 논리가 objective를 homogeneous하게 셋팅하므로 굉장히 좋은 특성이라고 언급하면서, generality를 잃지않고 항상 ${\color{red}\alpha^2_t+\sigma^2_t=1}$로 셋팅되도록 할 수 있다고 합니다.
예를 들어 기존의 $\alpha_t$와 $\sigma_t$를 아래와 같이 reparametrization을 진행한다고 합시다.
$$\begin{aligned}
\hat{\alpha}_t&=\frac{\alpha_t}{\sqrt{\alpha^2_t+\sigma^2_t}}\\
\hat{\sigma}_t&=\frac{\sigma_t}{\sqrt{\alpha^2_t+\sigma^2_t}}\\
\hat{\boldsymbol{x}}_t&=\hat{\alpha}_t\boldsymbol{x}_0+\hat{\sigma}_t\boldsymbol{z}&=\frac{\boldsymbol{x}_t}{\sqrt{\alpha^2_t+\sigma^2_t}}
\end{aligned}$$
그러면 기존의 $\alpha_t$와 $\sigma_t$, 그리고 새로운 $\hat{\alpha}_t$와 $\hat{\sigma}_t$는 아래를 만족합니다.
$$\begin{aligned}
\alpha^2_t+\sigma^2_t&=(\alpha^2_t+\sigma^2_t)(\hat{\alpha}_t^2+\hat{\sigma}_t^2)&=\alpha^2_t+\sigma^2_t\\
\hat{\alpha}_t^2+\hat{\sigma}_t^2&=1
\end{aligned}$$
이제 이런 상황에서 아래와 같은 특징을 가집니다.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
- $\boldsymbol{x}_0$를 예측해야하는 $\boldsymbol{D}_\theta$는 원래 아래와 같았던 식입니다.
$$\boldsymbol{D}_\theta(\boldsymbol{x}_t,t)={\color{blue}c_{skip}(t)}\boldsymbol{x}_t+{\color{blue}c_{out}(t)}{\color{red}\boldsymbol{F}_\theta(}{\color{blue}c_{in}(t)}\boldsymbol{x}_t,{\color{blue}c_{noise}(t)}{\color{red})}$$
각각 파라미터에 실제 파라미터를 넣고 위와 같은 reparametrization을 통해 계산해보면 아래와 같이 변합니다.
$$\boldsymbol{D}_\theta(\boldsymbol{x}_t,t)={\color{OliveGreen}{\color{OliveGreen}\hat{\sigma}_t}\hat{\boldsymbol{x}}_t}{\color{OliveGreen}-\hat{\alpha}_t\sigma_d}{\color{red}\boldsymbol{F}_\theta(}\frac{\color{OliveGreen}\hat{\boldsymbol{x}}_t}{\color{OliveGreen}\sigma_d},{\color{blue}c_{noise}(t)}{\color{red})}$$ - Loss는 원래 아래와 같았습니다.
$$\mathcal{L}_{Diff}=\mathbb{E}_{\boldsymbol{x}_0,\boldsymbol{z},t}\left[w(t){\color{blue}c^2_{out}(t)}\left\|\boldsymbol{F}_\theta\left({\color{blue}c_{in}(t)}{\boldsymbol{x}}_t,c_{noise}(t)\right)-\frac{{\color{blue}c_{skip}(t)}\alpha_t\boldsymbol{x}_0-(1-{\color{blue}c_{skip}(t)}\sigma_t)\boldsymbol{z})}{\color{blue}c_{out}(t)}\right\|^2_2\right]$$
위와 같은 reparametrization을 통해 계산해보면 아래와 같이 변합니다.
$$\mathcal{L}_{Diff}=\mathbb{E}_{\boldsymbol{x}_0,\boldsymbol{z},t}\left[w(t){\color{red}\hat{\alpha}_t^2}\left\|\sigma_d\boldsymbol{F}_\theta\left(\frac{\hat{\boldsymbol{x}}_t}{\sigma_d},c_{noise}(t)\right)-(\hat{\alpha}_t\boldsymbol{z}-\hat{\sigma}_t\boldsymbol{x}_0)\right\|^2_2\right]$$ - DPM Solver++와 같은 sampler에 적용할 때, 원래 $\lambda_t=log\frac{\alpha_t}{\sigma_t}$일 때 아래와 같은 식입니다.
$$\boldsymbol{x}_t=\frac{\sigma_t}{\sigma_s}\boldsymbol{x}_s+\sigma_t\int^{\lambda_t}_{\lambda_s}e^\lambda\boldsymbol{D}_\theta(\boldsymbol{x}_\lambda, \lambda)\mathrm{d}\lambda$$
$\frac{\boldsymbol{x}_t}{\sigma_t}=\frac{\hat{\boldsymbol{x}}_t}{\hat{\sigma}_t}$와 $\lambda_t=log\frac{\hat{\alpha}_t}{\hat{\sigma}_t}:=\hat{\lambda}_t$라는 사실을 활용해, 다시 변환해보면 아래와 같이 변합니다.
$$\boldsymbol{x}_t=\frac{\color{OliveGreen}\hat{\sigma}_t}{\color{OliveGreen}\hat{\sigma}_s}{\color{OliveGreen}\hat{\boldsymbol{x}}_s}+{\color{OliveGreen}\hat{\sigma}_t}\int^{\color{OliveGreen}\hat{\lambda}_t}_{\color{OliveGreen}\hat{\lambda}_s}e^{\color{OliveGreen}\hat{\lambda}}\boldsymbol{D}_\theta({\color{OliveGreen}\hat{\boldsymbol{x}}_{\hat{\lambda}}}, {\color{OliveGreen}\hat{\lambda}})\mathrm{d}{\color{OliveGreen}\hat{\lambda}}$$
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
위와 같이 reparametrization을 통한 $\hat{\alpha}_t$와 $\hat{\sigma}_t$를 noise schedule하고, reparametrization을 진행한 후의 $\hat{\boldsymbol{x}}_t$을 활용해 Sampling을 진행하더라도 성능에는 변함이 하나도 없습니다.
다시말하면, timestep t에서의 $(\alpha_t,\sigma_t,\boldsymbol{x}_t)$를 얻기 위한 diffusion process는 항상 $\sqrt{\alpha^2_t+\sigma^2_t}$로 나눠지며, $\hat{\alpha}^2_t+\hat{\sigma}^2_t=1$를 만족하는 $(\hat{\alpha}_t,\hat{\sigma}_t,\hat{\boldsymbol{x}}_t)$를 얻기 위한 diffusion process는 "동일하다"고 봐도 된다는 것입니다.
** 유일하게 다른것은 위 Loss에 표현된 $w(t){\color{red}\hat{\alpha}_t^2}$입니다.
자 이제 ${\color{red}\hat{\alpha}_t^2+\hat{\sigma}_t^2=1}$를 만족하는 상황에서는, $\hat{t}$를 $\hat{t}\in[0,\frac{\pi}{2}]$에서 아래와 같이 정의할 수 있습니다.
$$\hat{t}:=arctan(\frac{\hat{\sigma}_t}{\hat{\alpha}_t})=arctan(\frac{{\sigma}_t}{{\alpha}_t})$$
위와 같이 timestep을 정하면 $\hat{t}\in[0,\frac{\pi}{2}]$에서 $\hat{t}$가 점진적으로 증가할 때, $t\in[0,T]$에서 $t$가 1대1 매핑으로 점진적으로 증가하면서 아래를 만족합니다.
$$\begin{aligned}
t&\rightarrow \hat{t}\\
p(t)&\rightarrow p(\hat{t})\\
\hat{\alpha}_t&=cos(\hat{t})\\
\hat{\sigma}_t&=sin(\hat{t})\\
\end{aligned}$$
또한 VDM에서나 EDM은 SNR을 기준으로 timestep을 정의하는데, $SNR(t)=\frac{\alpha^2_t}{\sigma^2_t}$였다.
근데 여기서는 SNR을 정의할 때, $\boldsymbol{x}_t=\alpha_t\boldsymbol{x}_0+\sigma_t\boldsymbol{z}_t$에서 $\boldsymbol{x}_0$를 constant $\sigma_d$로 rescale한다고 생각하면 결국 아래와 같으므로, data variance에 무관하게 SNR을 정할 수 있어 좋은 성능을 보인다.
$$\widehat{SNR}(t)=\frac{\alpha^2_t\sigma^2_d}{\sigma^2_t}=\frac{1}{tan^2(t)}$$
이렇게 정의된 상황에서는 Loss가 아래와 같이 변동됩니다.
$$\mathcal{L}_{Diff}=\mathbb{E}_{\boldsymbol{x}_0,\boldsymbol{z}}\left[\underbrace{\color{red}\int^{\frac{\pi}{2}}_0p(\hat{t})w(\hat{t})cos^2(\hat{t})}_{\text{training weightning}}\left\|\underbrace{\sigma_d\boldsymbol{F}_\theta\left(\frac{\color{red}\hat{\boldsymbol{x}}_{\color{red}\hat{t}}}{\sigma_d},c_{noise}({\color{red}\hat{t}})\right)-({\color{red}cos({\hat{t}}})\boldsymbol{z}-{\color{red}sin(\hat{t})}\boldsymbol{x}_0)}_{\text{independent from }\alpha_t\text{ and }\sigma_t}\right\|^2_2{\color{red}\mathrm{d}\hat{t}}\right]$$
위 식을 보면, noise schedule의 영향이 결국 weighting에 담기며, 오른쪽의 $\mathcal{l}_2$ Loss는 $\alpha_t$, $\sigma_t$와 독립적인 것을 알 수 있습니다.
따라서 결과적으로 TrigFlow는 아래와 같은 식을 갖게 됩니다.
$$\begin{aligned}
\boldsymbol{x}_t&=cos(t)\boldsymbol{x}_0+sin(t)\boldsymbol{z}&\text{ for }t\in [0,\frac{\pi}{2}]\\
\frac{\mathrm{d}}{\mathrm{d}t}\boldsymbol{x}_t&=-sin(t)\boldsymbol{x}_0+cos(t)\boldsymbol{z}
\end{aligned}$$
또한 위에서 EDM의 파라미터는 $\hat{\boldsymbol{x}}_t=\frac{\boldsymbol{x}_t}{\sqrt{\alpha^2_t+\sigma^2_t}}$ 정의와 $\hat{\sigma}_t=sin(\hat{t})=\frac{\sigma_t}{\sqrt{\alpha^2_t+\sigma^2_t}}$, $\hat{\alpha}_t=cos(\hat{t})=\frac{\alpha_t}{\sqrt{\alpha^2_t+\sigma^2_t}}$에 의해서 아래와 같이 정리됩니다.
** ... 필자는 아직 ${\color{blue}c_{skip}(t)}$이 $sin(t)$여야할 것 같은데, 혹시 아래와 같이 변경되는 원인을 찾으시면 말씀해주세요..
$$\begin{aligned}
\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)&={\color{blue}c_{skip}(t)}\boldsymbol{x}_t+{\color{blue}c_{out}(t)}{\color{red}\boldsymbol{F}_\theta(}{\color{blue}c_{in}(t)}\boldsymbol{x}_t,{\color{blue}c_{noise}(t)}{\color{red})}\\
{\color{blue}c_{skip}(t)}&=cos(t)\\
{\color{blue}c_{out}(t)}&=-\sigma_dsin(t)\\
{\color{blue}c_{in}(t)}&=1/\sigma_d\\
{\color{blue}c_{noise}(t)}&=?
\end{aligned}$$
위와 같은 TrigFlow formulation은 아래와 같은 특징을 갖습니다.
- EDM의 DM process formulation을 따릅니다.
- 수식을 살펴보면 Flow Matching의 special case입니다.
** 궁금하시면 아래 더보기를 참조하세요 - 결국 EDM을 활용했지만 V-Prediction과 parametrization이 비슷합니다.
** 궁금하시면 아래 더보기를 참조하세요 - Trigonometric Interpolant와 비슷하지만 데이터 분포 $p_d$에 대한 표준편차 $\sigma_d$에 대해 수정되었습니다.
** Building normalizing flows with stochastic interpolants (ICLR'23)
----------------------------------------------------------------
<Velocity의 정의와 TrigFlow와의 관계>
v-prediction에서는 network의 target이 아래와 같았습니다.
$$\boldsymbol{v}=\alpha_t\epsilon-\sigma_t\boldsymbol{x}$$
이 식이 왜 TrigFlow와 비슷한지 보기 전에 정의된 과정을 살펴보겠습니다.
$\sigma_t$와 $\alpha_t$에 대한 parameterization을 SNR대신에 아래와 같이 각도 $\phi_t$로 표현할 수 있습니다.
$$\begin{aligned}
\phi_t&=arctan(\sigma_t/\alpha_t) \\
\sigma_t&=sin(\phi) \\
\alpha_t&=cos(\phi)\\
z_\phi&=cos(\phi)x+sin(\phi)\epsilon
\end{aligned}$$
이제 $z_\phi$의 velocity인 $v_\phi$는 아래와 같습니다.
$$\begin{aligned}
v_\phi&=\frac{dz_\phi}{d\phi}\\
&=cos(\phi)\epsilon-sin(\phi)x\\
\epsilon&=sin(\phi)z_\phi+cos(\phi)v_\phi\\
x&=cos(\phi)z_\phi-sin(\phi)v_\phi
\end{aligned}$$
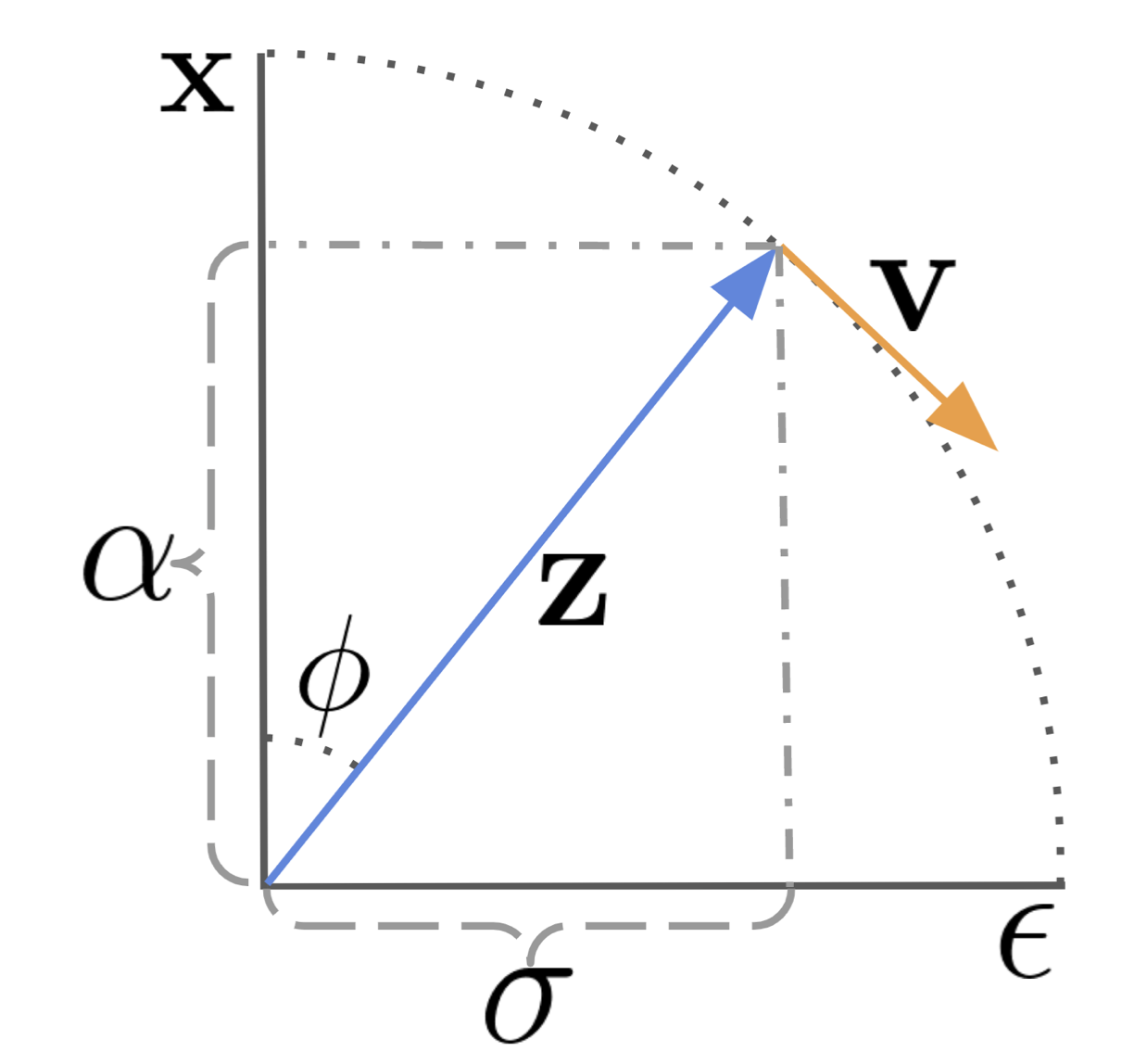
이 때, 위 그림과 같이 z가 $\phi_1$에서 $\phi_2$로 이동하면, velocity $v_\phi$를 포함한 수식으로 아래와 같이 정리할 수 있고, 결과적으로 velocity를 예측하면 이동하고 난 위치의 z를 찾아낼 수 있다는 것을 알 수 있습니다.
$$z_{\phi_{2}}=cos(\phi_{2}-\phi_{1})z_{\phi_{1}}+sin(\phi_{2}-\phi_{1})\hat{v}_\theta(z_{\phi_{1}})$$
따라서 위와 같은 정의에 따라, 결과적으로 denoising model $\hat{x}_\theta(x_t;t)$에 대한 표현으로 나타내면 아래와 같이 velocity를 통해 denoised 결과를 예측해낼 수 있습니다.
$$\hat{x}=\alpha_tz_t-\sigma_t\hat{v}_\theta(z_t)$$
근데 TrigFlow에서는 $\boldsymbol{x}_t=cos(t)\boldsymbol{x}_0+sin(t)\boldsymbol{z}$이기 때문에, 위 velocity와 비슷하다는 것을 알 수 있습니다.
----------------------------------------------------------------
----------------------------------------------------------------
<Flow Matching과 TrigFlow>
$\alpha_t$와 $\sigma_t$를 조정하는 것은 noise schedule이라고 합니다.
- Variance Preserving : DDPM, Score-based
- Variance Exploding : Score-based, EDM
- Cosine Schedule : Improved-DM
- Conditional Optimal Transport Path : Flow Matching
기존에 Flow Matching에서는 아래와 같이 정의했던 것을 기억하실 겁니다.
** 아래에서 $\alpha_0=1,\alpha_t=0,\sigma_0=0,\sigma_T=1$입니다.
$$\begin{aligned}
\boldsymbol{x}_t&=\alpha_t\boldsymbol{x}_0+\sigma_t\boldsymbol{z}\\
\alpha_t&=1-t\\
\sigma_t&=t\\
\boldsymbol{v}_t&=\frac{\mathrm{d}\alpha_t}{\mathrm{d}t}\boldsymbol{x}_0+\frac{\mathrm{d}\sigma_t}{\mathrm{d}t}\boldsymbol{z}
\end{aligned}$$
그리고 이 velocity를 학습하는 loss는 아래와 같습니다.
$$\mathbb{E}_{\boldsymbol{x}_0,\boldsymbol{z},t}\left[w(t)\left\|\boldsymbol{v}_\theta(x_t,t)-\boldsymbol{v}_t(x_t|x_0)\right\|^2_2\right]$$
이렇게 학습된 $\boldsymbol{v}_\theta(x_t,t)$를 활용해 아래와 같은 PF-ODE를 통해 reverse로 진행을 하는 것입니다.
$$\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}=\boldsymbol{v}_\theta(x_t,t)$$
근데 이 Flow Matching은 위를 활용한 noise schedule 때문에 성능이 잘 나왔던 것 같지만, 사실 다른 noise schedule로도 변경이 가능합니다.
해당 논문이 잘되었던 것은 weighting 기법과 DPM-Solver같은 개선된 sampler 때문이지 Straight Path 때문만이여서만은 아니었던 것이라는 것입니다.
TrigFlow는 $\alpha_t=cos(t)$와 $\sigma_t=sin(t)$라는 noise schedule을 활용하고, PF-ODE의 식은 아래와 같았던 것을 기억하실 겁니다.
$$\sigma_d\boldsymbol{F}_\theta\left(\frac{\boldsymbol{x}_{t}}{\sigma_d},c_{noise}({t})\right)$$
이는 위에서 보았던 Flow Matching의 diffusion ODE와 비슷한 형태를 가지는 것을 볼 수 있고, 실제로 Loss도 Flow Matching과 비슷한 형태를 가집니다.
이를 통해 TrigFlow는 Flow Matching과 비슷하다는 것을 알 수 있고, 본 논문에서는 TrigFlow가 Flow Matching의 special case라고 하고 있습니다.
----------------------------------------------------------------
위 특징을 보면 1. EDM의 formulation을 따르면서도, 2. Flow Matching의 special case이므로 각각의 장점을 취하면서도 아래를 가능하게 합니다.
- 1. Diffusion Process
- 2. PF-ODE
- 3. Diffusion Training Objective
- 4. CM Parametrization
1. Diffusion Process
데이터 $\boldsymbol{x}_0\sim p_d(\boldsymbol{x}_0)$와 노이즈 $\boldsymbol{z}\sim \mathcal{N}(\boldsymbol{0}, \sigma^2_d\boldsymbol{I})$가 있을 때, forward perturbation은 아래와 같은 식으로 진행됩니다.
$$\boldsymbol{x}_t=cos(t)\boldsymbol{x}_0+sin(t)\boldsymbol{z}\text{ for }t\in [0,\frac{\pi}{2}]$$
특히, prior sample $\boldsymbol{x}_{\frac{\pi}{2}}\sim \mathcal{N}(\boldsymbol{0}, \sigma_d^2\boldsymbol{I})$입니다.
2. PF-ODE
reverse에 활용되는 DM의 결과는 아래와 같을 것이고,
$$\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)=cos(t)\boldsymbol{x}_t-sin(t)\sigma_d\boldsymbol{F}_\theta(\frac{\boldsymbol{x}_t}{\sigma_d},c_{noise}(t))$$
이에 대한 PF-ODE는 아래와 같이 쉽게 구해집니다.
$$\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}=\sigma_d\boldsymbol{F}_\theta(\frac{\boldsymbol{x}_t}{\sigma_d},c_{noise}(t))$$
3. Diffusion Training Objective
TrigFlow에서의 Loss는 결국 아래와 같이 사용될 것입니다.
** $\boldsymbol{v}_t=cos(t)\boldsymbol{z}-sin(t)\boldsymbol{x}_0$로, tangent target입니다.
$$\begin{aligned}
\mathcal{L}_{Diff}(\theta)&=\mathbb{E}_{\boldsymbol{x}_0,\boldsymbol{z},t}\left[\left\|\sigma_d\boldsymbol{F}_\theta(\frac{\boldsymbol{x}_t}{\sigma_d},c_{noise}(t))-\boldsymbol{v}_t\right\|^2_2\right]\\
&=\mathbb{E}_{\boldsymbol{x}_0,\boldsymbol{z}}\left[{\color{red}\int^{\frac{\pi}{2}}_0w(t)}\left\|{\sigma_d\boldsymbol{F}_\theta\left(\frac{\boldsymbol{x}_{t}}{\sigma_d},c_{noise}({t})\right)-({cos({t}})\boldsymbol{z}-{sin(t)}\boldsymbol{x}_0)}\right\|^2_2{\mathrm{d}t}\right]
\end{aligned}$$
4. CM Parametrization
결국 위 parametrization에 의해 TrigFlow는 아래와 같은 form을 가지므로, EDM과 비슷합니다.
$$\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)=cos(t)\boldsymbol{x}_t-sin(t)\sigma_d\boldsymbol{F}_\theta(\frac{\boldsymbol{x}_t}{\sigma_d},c_{noise}(t))$$
따라서 EDM의 formulation을 활용하는 CM은 당연히 가능합니다.
하지만 boundary condition $\boldsymbol{f}_\theta(\boldsymbol{x},0)=\boldsymbol{x}$를 만족해야하는데, 위 PF-ODE의 single-step solution으로 parametrization하면 위 조건을 충분히 만족한다고 볼 수 있습니다.
$$\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}=\sigma_d\boldsymbol{F}_\theta(\frac{\boldsymbol{x}_t}{\sigma_d},c_{noise}(t))$$
b. sCM
원래 continuous-time CM을 학습하는 것은 굉장히 unstable하므로 discrete-time CM보다 성능이 좋지 않은데, 이를 위해 앞서 소개한 TrigFlow 프레임워크 기반으로한 이론적인 개선 방법을 아래의 세개의 측면에서 진행합니다.
- Parametrization
- Network Architecture $c_{noise}(t)=t$
- Training Objectives
이렇게 만들어진 모델을 본 논문에서는 sCM(simple, stable, scalable CM)이라고 부릅니다.
1. Parametrization
원래 continuous CM의 핵심은 tagent function $\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}$에 의존한 아래의 식입니다.
$$\nabla_\theta\mathbb{E}_{\boldsymbol{x}_t,t}[w(t)\boldsymbol{f}_\theta^\top(\boldsymbol{x}_t,t){\color{red}\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}]$$
위 tangent function에 TrigFlow formulation을 적용하면 아래와 같이 바뀝니다.
** $\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}$는 pretrained DM에서 사용하는 PF-ODE일수도 있고, Isolation으로 학습되는 unbiased estimator일수도 있습니다.
$$\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}=-cos(t) \left( {\color{blue}\sigma_d \boldsymbol{F}_{\theta^-}}(\frac{\boldsymbol{x}_t}{\sigma_d},t)-{\color{blue}\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}}\right)-sin(t)\left({\color{blue}\boldsymbol{x}_t}+\sigma_d{\color{red}\frac{\mathrm{d}\boldsymbol{F}_{\theta^-}(\frac{\boldsymbol{x}_t}{\sigma_d},t)}{\mathrm{d}t}}\right)$$
이제 학습을 안정시키기 위해서는 위 tagent function이 모든 time step에서 stable해야하는데, 본 논문에서는 실험적으로 위 식의 파란색 부분은 상대적으로 안정적이었다고 합니다.
그럼 위 식에서 남은 부분은 위 빨간 부분이고 이를 정리하면 아래와 같습니다.
$$sin(t)\frac{\mathrm{d}\boldsymbol{F}_{\theta^-}}{\mathrm{d}t}={\color{blue}sin(t)\nabla_{\boldsymbol{x}_t}\boldsymbol{F}_{\theta^-}\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}}+{\color{red}sin(t)\delta_t\boldsymbol{F}_{\theta^-}}$$
위 식에서 또 분석을 해보니 파란부분은 잘 conditioned되지만 위 빨간 부분이 결국에 instability의 근본 원인이었고 이를 정리하면 아래와 같다고 합니다.
** $emb()$는 time embedding을 의미하며, 일반적으로 Positional embedding이나 Fourier embedding을 활용합니다.
$$\sin(t)\delta_t\boldsymbol{F}_{\theta^-}={\color{OliveGreen}sin(t)}\frac{\color{OliveGreen}\delta c_{noise}(t)}{\delta t}\cdot\frac{\color{Purple}\delta emb(c_{noise})}{\delta c_{noise}}\cdot\frac{\delta \boldsymbol{F}_{\theta^-}}{emb(c_{noise})}$$
위 식의 빨간 부분은 아래에서 다룰 계획입니다.
2. Network Architecture $c_{noise}(t)=t$
대부분의 존재하는 CM은 EDM formulation을 따르므로 쉽게 TrigFlow formulation으로 변경할 수 있는데, timestep을 변경하는 $c_{noise}(t)$는 아래와 같이 표현이 가능합니다.
$$c_{noise}(t)=log(\sigma_dtan(t))$$
이 식을 위에서 instability의 근본원인이었던 식 중 초록색으로 표현된 ${\color{OliveGreen}sin(t)\delta c_{noise}(t)}$에 적용해 보니 아래와 같은 식으로 표현할 수 있고, 식을 보면 알 수 있듯이 $t\rightarrow\frac{\pi}{2}$일 때마다 계속해서 blow up하는 문제가 있다는 것을 발견했습니다.
$$\sin(t)\cdot \delta_tc_{noise}(t)=1/cos(t) $$
그래서 본 논문에서는 timestep 변환을 아래와 같이 진행했다고 합니다.
$$c_{noise}(t)=t$$
다음으로, 기존의 일반적인 Positional Embedding인 ${\color{Purple}emb()}$함수와 미분 값 ${\color{Purple}\delta_cemb(c)}$은 아래와 같았습니다
$$\begin{aligned}
emb(c)&=sin(s\cdot2\pi\omega\cdot c+\phi)\\
\delta_cemb(c)&=s\cdot 2\pi\omega cos(s\cdot 2\pi\omega\cdot c +\phi)
\end{aligned}$$
근데 위 식에서 Fourier scale $s$가 클수록 미분값이 굉장히 크게 진동하기 때문에 위에서 instability의 근본원인이었던 식 중 보라색으로 표현된 부분의 instability를 유발하고, 다른 논문에서도 이런 문제가 발견되기도 했습니다.
** Improved techniques for training consistency models (arxiv’23)
따라서 본 논문에서는 이를 피하기 위해 $s\approx0.02 $정도로 positional embedding을 활용했다고 합니다.
다음으로, 앞서의 문제를 발견한 논문에서 아래 식으로 표현 가능한 AdaGN Layer를 활용하는 것이 CM 학습에 부정적인 영향을 끼친다는 것을 발견했습니다.
** Improved techniques for training consistency models (arxiv’23)
$$y=norm(\boldsymbol{x})\odot \boldsymbol{s}(t)\cdot \boldsymbol{b}(t)$$
그래서 본 논문에서는 아래와 같이 $pnorm()$을 활용한 Adaptive Double Normalization 기법을 제안했고, 실험적으로 봤을 때 AdaGN이 instability없이 CM학습이 잘 되었다고 합니다.
** $pnorm()$은 pixel normalization을 의미합니다.
$$y=norm(\boldsymbol{x})\odot {\color{red}pnorm(}\boldsymbol{s}(t){\color{red})}\cdot {\color{red}pnorm(}\boldsymbol{b}(t){\color{red})}$$
아래 그림은 이런 1. Parametrization와 2. Network Architecture $c_{noise}(t)=t$를 통해 CIFAR-10에서 학습했을 때 continuous-CM의 학습에서 활용하는 tagent function $\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}=\nabla_{\boldsymbol{x}}\boldsymbol{f}_{\theta^-}\cdot\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}+\delta_t\boldsymbol{f}_{\theta^-}$의 두 항에 대한 EDM과 TrigFlow의 결과를 보입니다.

$c_{noise}(t)$ 뿐 아니라, Positional Embedding을 통해, timestep $t$에 대해 $\boldsymbol{x}_t$와 t에 대한 미분 모두 stable한 것을 볼 수 있습니다.
3. Training Objectives
기존의 continuous CM의 loss에 활용되는 gradient는 아래와 같았습니다.
$$\begin{aligned}
&\nabla_\theta\mathbb{E}_{\boldsymbol{x}_t,t}[w(t)\boldsymbol{f}_\theta^\top(\boldsymbol{x}_t,t){\color{red}\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}]&\\
{\color{red}\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}&=\nabla_{\boldsymbol{x}_t}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}+\delta_t\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)&\text{ (tangent of }\boldsymbol{f}_{\theta^-}\text{ at }(\boldsymbol{x}_t,t)\text{)}
\end{aligned}$$
하지만 위 식에 TrigFlow formulation을 적용하고 나면 아래와 같이 변화됩니다.
$$\nabla_\theta\mathbb{E}_{\boldsymbol{x}_t,t}\left[-{\color{red}w(t)}\sigma_dsin(t)\boldsymbol{F}_\theta^\top (\frac{\boldsymbol{x}}{\sigma_d},t){\color{red}\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}\right]$$
하지만 본 논문에서는 아래와 같이 위 빨간 부분에 대해 추가적으로 stability를 올리기 위한 추가 테크닉을 보입니다.
- a. Tangent Normalization
- b. Adaptive Weighting
- c. Diffusion Finetuning & Tangent Warmup
이를 하나씩 보이겠습니다.
a. Tangent Normalization
앞서서 언급한 바와 같이 대부분의 CM 학습의 gradient variance는 tangent function $\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}$으로부터 발생하는데, 아예 tangent function자체를 아래와 같이 normalize하기도 한다고 합니다.
** c는 실제 실험적으로 선택해 0.1로 했습니다.
$$\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}\rightarrow \frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}/\left(\|\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}\|+c\right)$$
또한 추가적으로 tangent자체를 [-1,1]로 clipping하는 방법도 추가할 수 있는데, 이는 위 gradient variance의 한도를 정할 수 있습니다.
아래 그림을 보시면 normalization과 clipping 모두 continuous-time CM의 학습의 상당한 향상이 있음을 확인할 수 있습니다.
** DM은 EDM2를 ImageNet(512x512)에서 학습한 모델을 활용했으며, 1step과 2step 모두 실험했습니다.

b. Adaptive Weighting
이전 논문에서는 weighting function인 $w(t)$를 manual하게 셋팅했었는데, 이는 서로 다른 데이터와 네트워크 아키텍처에 대해 suboptimal이 될 수 있습니다.
** Improved techniques for training consistency models (arxiv’23)
따라서 기존 EDM2 논문과 비슷하게, CM에 맞게 adaptive weighting function을 학습하는 것을 제안했고 이를 통해 hyperparameter tuning의 어려움을 줄이고 기존 manual한 weighting function보다 높은 성능을 얻을 수 있었다고 합니다.
** Analyzing and improving the training dynamics of diffusion models (CVPR’24)
본 논문에서는 Adaptive Weighting의 핵심은 $\boldsymbol{y}$라는 임의의 벡터가 $\theta$와 독립적일 때 아래와 같이 표현할 수 있다는 것이라고 합니다.
$$\nabla_\theta\mathbb{E}[\boldsymbol{F}_\theta^\top\boldsymbol{y}]=\frac{1}{2}\nabla_\theta\mathbb{E}[\|\boldsymbol{F}_\theta-\boldsymbol{F}_{\theta^-}+\boldsymbol{y}\|^2_2]$$
위 loss에서 $\boldsymbol{y}$는 결국 $\boldsymbol{y}=-w(t)\sigma_dsin(t)\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}}{\mathrm{d}t}$일 것이고, 이를 활용해 위에서 보였던 식을 아래와 같이 변경합니다.
** 이렇게 함으로써 EDM2와 같이 adaptive weighting function을 학습할 수 있게 되며, 모든 timestep에서 MSE loss의 variance를 줄일 수 있다고 합니다.
$$\begin{aligned}
\nabla_\theta\mathbb{E}_{\boldsymbol{x}_t,t}\left[\boldsymbol{F}_\theta^\top (\frac{\boldsymbol{x}}{\sigma_d},t)(-{w(t)}\sigma_dsin(t)){\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}\right]\\
\nabla_\theta\mathbb{E}_{\boldsymbol{x}_t,t}\left[\boldsymbol{F}_\theta(\frac{\boldsymbol{x}}{\sigma_d},t)-\boldsymbol{F}_{\theta^-} (\frac{\boldsymbol{x}}{\sigma_d},t)-{w(t)}\sigma_dsin(t){\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}\right]
\end{aligned}$$
위 식에서의 $w(t)$는 앞으로 사용할 weighting function의 prior라고 볼 수 있는데, 본 논문에서는 아래와 같이 prior weighting을 활용하는 것이 training variance를 줄일 수 있었다고 합니다.
$$w(t)=\frac{1}{\sigma_dtan(t)}$$
이를 적용하면 위 Gradient가 아래와 같이 변경됩니다.
$$\nabla_\theta\mathbb{E}_{\boldsymbol{x}_t,t}\left[\boldsymbol{F}_\theta(\frac{\boldsymbol{x}}{\sigma_d},t)-\boldsymbol{F}_{\theta^-} (\frac{\boldsymbol{x}}{\sigma_d},t)-{\color{red}cos(t)}{\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}\right]$$
이제 위 식을 통해 adaptive weighting function $w_\phi(t)$와 네트워크 $\boldsymbol{F}_\theta$를 학습하는 Loss는 아래와 같이 나타낼 수 있습니다.
** $D$는 $\boldsymbol{x}_0$의 차원이며, timestep tan(t)는 EDM과 같이 log-Normal Distribution $e^{\sigma_dtan(t)}\sim\mathcal{N}(P_{mean},P^2_{std})$을 활용해 샘플링했다고 합니다.
$$\mathcal{L}_{sCM}(\theta,\phi):=\mathbb{E}_{\boldsymbol{x}_t,t}\left[\frac{e^{\color{red}w_\phi(t)}}{D}\left\|\boldsymbol{F}_\theta(\frac{\boldsymbol{x}_t}{\sigma_d},t)-\boldsymbol{F}_{\theta^-}(\frac{\boldsymbol{x}_t}{\sigma_d},t)-cos(t)\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}\right\|^2_2-{\color{red}w_\phi(t)}\right]$$
아래 그림을 보시면 adaptive weighting을 사용했을 때 FID가 훨씬 낮은 것을 볼 수 있습니다.
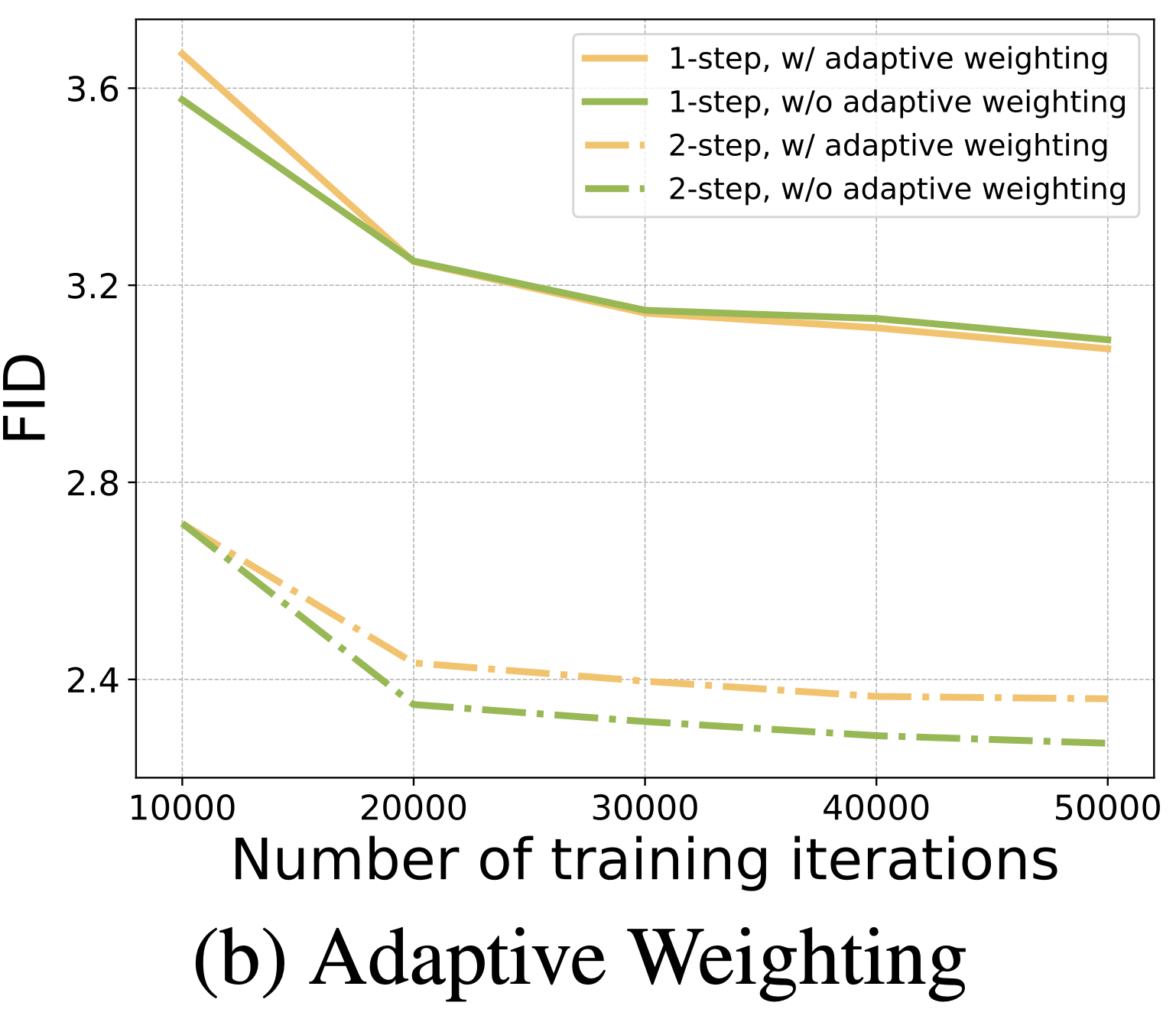
c. Diffusion Finetuning & Tangent Warmup
기존 CM과 같이 pre-trained DM을 활용한 Consistency Distillation은 convergence의 속도를 가속화할 수 있습니다.
또한 앞서서 tangent function이 아래와 같이 두개의 파트로 나뉘고, 파란부분은 상대적으로 stable하지만 빨간부분은 instability를 유발하는 부분이라고 했었습니다.
$$\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}=-{\color{blue}cos(t) \left( {\sigma_d \boldsymbol{F}_{\theta^-}}(\frac{\boldsymbol{x}_t}{\sigma_d},t)-{\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}}\right)}-{\color{red}{sin(t)\left({\boldsymbol{x}_t}+\sigma_d\frac{\mathrm{d}\boldsymbol{F}_{\theta^-}(\frac{\boldsymbol{x}_t}{\sigma_d},t)}{\mathrm{d}t}\right)}}$$
이 문제를 줄이기 위해서 추가적으로 위 두번째 빨간 term을 점진적으로 warm up하도록 하기 위해 아래와 같이 r이라는 파라미터를 추가해 10k의 iteration동안 0.0에서 1.0으로 점진적으로 증가하도록 해주었습니다.
** 생성 모델에서는 전체 데이터가 다 돌아감을 의미하는 epoch보다는, 진행률을 의미하는 iteration을 기준으로 주로 나타내곤 합니다.
$$\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}=-{cos(t) \left( {\sigma_d \boldsymbol{F}_{\theta^-}}(\frac{\boldsymbol{x}_t}{\sigma_d},t)-{\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}}\right)}-{{{\color{red}\boldsymbol{r}sin(t)}\left({\boldsymbol{x}_t}+\sigma_d\frac{\mathrm{d}\boldsymbol{F}_{\theta^-}(\frac{\boldsymbol{x}_t}{\sigma_d},t)}{\mathrm{d}t}\right)}}$$
결과적으로 위 모든 기술을 합쳤을 때 discrete-time CM과 continuous-time CM의 학습이 모두 향상되었으며, 특히 discrete-time에서는 discretization step N이 증가할수록 discretization error가 줄어 샘플의 퀄리티가 증가 했다고 합니다.
아래 그림을 보면 실제 그 현상을 확인할 수 있지만, 반대로 N>1024 정도로 너무 클때는 오히려 numerical precision 문제로 성능이 더 안좋아졌습니다.
또한 continuous-time에서는 오히려 이 모든 것보다 성능이 좋았습니다.

최종적으로 discrete-time CM을 학습하는 알고리즘은 아래와 같습니다.

continuous-time CM을 학습하는 알고리즘은 아래와 같습니다.

c. Scaling-up sCM
다음으로 위에서 소개한 sCM을 다양한 데이터셋을 활용해 large-scale로 scale-up하는 과정을 소개하려고 합니다.
보통 large-scale DM을 학습할 때는 half-precision(FP16)과 Flash Attention을 활용하곤 하는데, continuous-time CM은 tangent인 $\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}}{\mathrm{d}t}$는 정확하게 계산해야하므로 아래와 같은 두가지가 과제입니다.
- 1. numerical precision을 향상시켜야한다.
- 2. 메모리 효율적으로 attention을 연산해야한다.
이에 대해 본 논문에서는 JVP(Jacobian-vector product) Rearrange를 활용합니다.
먼저, Loss에서 가장 중요한 tangent함수는 아래와 같았습니다.
$$\begin{aligned}
\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}}{\mathrm{d}t}&=\nabla_{\boldsymbol{x}_t}\boldsymbol{f}_{\theta^-}\cdot\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}&&+\delta_t\boldsymbol{f}_{\theta^-}\\
\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}&=\nabla_{\boldsymbol{x}_t}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)\cdot\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}&&+\delta_t\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)
\end{aligned}$$
근데 결국 아래와 같이 TrigFlow formulation을 하고나면
$$\begin{aligned}
\boldsymbol{f}_\theta(\boldsymbol{x}_t,t)&={\color{blue}c_{skip}(t)}\boldsymbol{x}_t+{\color{blue}c_{out}(t)}{\color{red}\boldsymbol{F}_\theta(}{\color{blue}c_{in}(t)}\boldsymbol{x}_t,{\color{blue}c_{noise}(t)}{\color{red})}\\
{\color{blue}c_{skip}(t)}&=cos(t)\\
{\color{blue}c_{out}(t)}&=-\sigma_dsin(t)\\
{\color{blue}c_{in}(t)}&=1/\sigma_d\\
{\color{blue}c_{noise}(t)}&=?
\end{aligned}$$
결국 아래와 같은 식을 구하는 것이 핵심일 것입니다. 이는 input vector $(\boldsymbol{x}_t,t)$와 tangent vector $(\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t},t)$에 대한 $\boldsymbol{F}_{\theta^-}(\frac{\cdot}{\sigma_d},\cdot)$을 JVP(Jacobian-vector product)를 통해 효율적으로 얻어내야 할것입니다.
$$\frac{\mathrm{d}\boldsymbol{F}_{\theta^-}}{\mathrm{d}t}=\nabla_{\boldsymbol{x}_t}\boldsymbol{F}_{\theta^-}\cdot\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t}+\delta_t\boldsymbol{F}_{\theta^-}$$
이 때, 본 논문에서는 실험적으로 t가 0이나 $\frac{\pi}{2}$에 가까울 때, tangent의 intermediate layer에서 overflow가 발생하는 것을 확인했다고 합니다.
그래서 numerical precision을 향상시키기 위해서는 tangent 연산을 rearrange해야 한다고 합니다.
다시 돌아가 Loss를 살펴보면, Loss는 아래와 같이 빨간 부분을 포함하고 있고, 이 빨간 부분 중 tangent $\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}$는 위에서 본 것 처럼 ${\color{blue}c_{out}(t)}$때문에 $sin(t)\frac{\mathrm{d}\boldsymbol{F}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}$와 비례합니다.
$$\mathcal{L}_{sCM}(\theta,\phi):=\mathbb{E}_{\boldsymbol{x}_t,t}\left[\frac{e^{w_\phi(t)}}{D}\left\|\boldsymbol{F}_\theta(\frac{\boldsymbol{x}_t}{\sigma_d},t)-\boldsymbol{F}_{\theta^-}(\frac{\boldsymbol{x}_t}{\sigma_d},t)-{\color{red}cos(t)\frac{\mathrm{d}\boldsymbol{f}_{\theta^-}(\boldsymbol{x}_t,t)}{\mathrm{d}t}}\right\|^2_2-{w_\phi(t)}\right]$$
따라서 결국 아래와 같이 JVP를 아래와 같이 rearrange할 수 있습니다.
$$cos(t)sin(t)\frac{\mathrm{d}\boldsymbol{F}_{\theta^-}}{\mathrm{d}t}=(\nabla_{\frac{\boldsymbol{x}_t}{\sigma_d}}\boldsymbol{F}_{\theta^-})\cdot(cos(t)sin(t)\frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t})+\delta_t\boldsymbol{F}_{\theta^-}\cdot(cos(t)sin(t)\sigma_d)$$
이렇게함으로써 위 언급한 overflow를 해결할 수 있고, FP16에서도 stable한 학습이 가능해집니다.
또한 기존의 Flash Attention는 GPU 메모리를 적게사용함으로써 빠른 학습을 가능하도록 해줬는데, JVP를 계산하지 못합니다.
그래서 본 논문에서는 위와 같은 방법으로 softmax self-attention과 forward pass에서의 JVP 모두 Flash Attention을 효율적으로 연산하도록 하는 방법을 제안합니다.
이를 통해 JVP연산을 위한 GPU메모리를 크게 줄일 수 있었다고 합니다.
3. Results
앞서의 Consistency Model의 두 가지를 본 논문에서는 아래와 같이 나눠 부릅니다.
- sCT(stable Consistency Training)
- sCD(stable Consistency Distillation)
continuous-time CM을 학습하고 scale-up할 때의 학습세팅은 아래와 같습니다.
- Data : CIFAR-10, ImageNet(64x64), ImageNet(5124x512)
- Initial Parameter Setting
- CIFAR-10 : Score-based SDE
- ImageNet(64x64), ImageNet(5124x512) : EDM2
- Timestep Setting (≒ 기존 CD)
- 2-step (sCT, sCD 모두)
- time step t = 1.1
- CFG
- (sCD) CFG를 위해 학습할 모델 $\boldsymbol{F}_\theta$에 추가 guidance scale $s\in[1,2]$를 넣어 학습했습니다.
- (sCD) distillation과정에서는 Teacher 모델에도 같은 CFG를 적용해주었습니다.
- (sCT) CFG를 테스트하지 않았습니다.
1. Training Compute
학습할 때 같은 batch size를 주고 effective compute per training을 계산해보니, sCD에서 학습할 모델의 training compute가 Teacher DM의 2배 정도가 되었다고합니다.
하지만 빠르게 converge해서 Teacher DM의 20%보다도 작은 training compute를 사용하면서도 비길만한 결과가 나왔다고 합니다.
sCD 학습은 finetuning시에 20k iteration이후에 높은 퀄리티의 샘플을 얻을 수 있었습니다.
2. vs Benchmarks
각각의 데이터셋에 대해 기존 방법들을 학습하고 FID, NFE(Number of Function Evaluations)를 측정해본 결과는 아래와 같습니다.


먼저 sCM은 기존의 few-step방법들보다는 더 좋은 결과를 얻을 수 있었으며, 다른 생성기법들보다도 성능이 좋거나 비길만했다고 합니다.
특히 비길만한 성능이 나온 경우에도, 기존 방법은 63steps가 필요하기 때문에 적은 step가 필요한 sCM의 성능이 더 좋습니다.
2-step sCM은 빠르게 teacher DM과의 FID 갭을 줄일 수 있었으며, 결과적으로 sCT와 sCD의 경우 각각 아래와 같은 특징을 가졌습니다.
- sCT : 작은 scale에서 더욱 효율적이었으며, 큰 scale에서는 높아진 variance의 안좋은 영향을 받았습니다.
- sCD : 작고 큰 scale 모두에서 consistent한 성능을 보였습니다.
3. Scaling Study
"학습 instability 없이 continuous-time CM을 scaling할 수 있는지"를 확인 하기 위해 EDM2(S, M, L, XL, XXL) configuration을 활용해 ImageNet(64x64), ImageNet(256x256)에서 학습했으며, 최적의 guidance scale에서 FID를 측정한 결과는 아래와 같습니다.

결과적으로 FLOPs가 증가할수록 sCT와 sCD는 샘플 퀄리티가 증가하는 것으로 보아, 두 방법 모두 scaling-up이 잘되는 것을 확인할 수 있습니다.
또한 sCD의 경우, 위와 같이 모델크기가 증가할수록 모델 크기에 따른 상대적인 차이가 유지되는 것을 보아, 본 논문에서는 "Teacher 모델과 비슷하게 유지되는 것"이며 Teacher 모델에 비례해서 scaling되는 것 같다고 합니다.
또한 scaling up될수록 Teacher 모델과의 절대적인 FID차이는 줄어듭니다.
마지막으로 sCT는 작은 resolution에서가 더 연산량 면에서 더 효율적이었다고 합니다.
4. vs VSD
VSD(Variational Score Distillation)기법은 또 다른 DM distillation 기법으로, high-resolution 이미지에 대한 scalablity를 보였습니다.
** Prolificdreamer: High-fidelity and diverse text-to-3d generation with variational score distillation (NIPS’24)
** One-step diffusion with distribution matching distillation (CVPR’24)
이번엔 one-step VSD를 EDM2-M configuration으로 학습하고, sCD와 비교해보았습니다.
아래 그림은 위 학습한 VSD와 sCD, 그리고 두 loss를 합쳐 학습한 VSD+sCD를 guidance scale에 따라 성능을 확인한 그림입니다.

먼저 VSD는 guidance scale이 증가함에 따라 fidelity가 증가(precision이 증가)하고, diversity가 감소(recall이 감소)하는 형태를 보였으며, 높은 guidance scale에서는 mode collapse가 발생한 것처럼 보입니다.
하지만 2-step sCD는 precision과 recall이 기존 teacher DM과 비슷한 정도로 그치며, 심지어 더 좋은 FID를 가진다고 합니다.
Flow Matching : https://arxiv.org/pdf/2301.12003 appendix A.2
