2024. 11. 10. 22:48ㆍDevelopers 공간 [Shorts]/Vision & Audio
<분류>
A. 수단
- OS/Platform/Tool : Linux, Kubernetes(k8s), Docker, AWS
- Package Manager : node.js, yarn, brew,
- Compiler/Transpillar : React, Nvcc, gcc/g++, Babel, Flutter
- Module Bundler : React, Webpack, Parcel
B. 언어
- C/C++, python, Javacsript, Typescript, Go-Lang, CUDA, Dart, HTML/CSS
C. 라이브러리 및 프레임워크 및 SDK
- OpenCV, OpenCL, FastAPI, PyTorch, Tensorflow, Nsight
1. What? (현상)
어떤 Data들을 특정 네트워크를 통과시킨 후에 얻은 embedding을 Data space위에 display하고 나면 해당 데이터의 네트워크에서의 특징들을 표현할 수 있어 다양하게 활용되곤 합니다.
이 방법을 정리해보고자 합니다.
2. Why? (원인)
- X
3. How? (해결책)
sklearn(scikit learn)은 python에서 scipy위에서 머신러닝을 분석할 때 활용하는 라이브러리로, 이를 활용하면 classification, regression, clustering, dimension reduction 등을 구현할 수 있습니다. 이를 활용한 두가지 방법을 보이겠습니다.
** SciPy(Scientific Python) : 수학, 과학 등의 엔지니어링에서 계산을 위한 라이브러리 입니다.
pip3 install sklearn prdc
apt-get install python3-tk
설명에 앞서 embedding은 아래의 numpy를 활용해 예로 만들어보겠습니다. 아래 예의 100은 데이터 수를 의미하며 500은 임베딩의 차원을 의미합니다.
import numpy as np
a = []
mu, sigma = 3.5, 0.3 # mean and standard deviation
for emb_dim in range(100):
a.append(np.random.normal(mu, sigma, 500))
b = []
mu, sigma = 5.5, 0.6 # mean and standard deviation
for emb_dim in range(100):
b.append(np.random.normal(mu, sigma, 500))
1. T-SNE(T-distributed Stochastic Neighbor Embedding)
https://scikit-learn.org/1.5/modules/generated/sklearn.manifold.TSNE.html
T-SNE는 고차원의 데이터를 저차원 영역으로 표현하기 위한 비선형 차원 축소 기법입니다.
기존의 의미 있는 차원을 "선택"하는 feature selection과 달리 고차원 데이터의 구조의 패턴을 유지하면서 축소를 가능하게 하며, 각 데이터 간의 거리를 최대한 보존하는 방식으로 축소하기 때문에 시각화할 때 사용합니다.

함수는 아래와 같습니다.
- embddings : [Data개수, Embedding 차원]
- embeddings_2d : [Data개수, 2]
from sklearn.manifold import TSNE
def dim_reduction(embeddings):
tsne = TSNE(n_components=2, random_state=42)
embeddings_2d = tsne.fit_transform(embeddings)
return embeddings_2d
그럼 이를 실행해 보겠습니다.
embeddings_2d= dim_reduction(a)
이렇게 만들어진 2D embedding을 plot해보겠습니다.
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 8))
plt.scatter(embeddings_2d[:, 0], embeddings_2d[:, 1], s=50, cmap='viridis', c=embeddings_2d[:,0], alpha=0.6)
for i, (x, y) in enumerate(embeddings_2d):
plt.annotate(str(i), (x, y), textcoords="offset points", xytext=(0,5), ha='center')
plt.title('Visualized embeddings')
plt.xlabel('t-SNE Component 1')
plt.ylabel('t-SNE Component 2')
plt.colorbar()
plt.savefig("output.png")
plt.show()
#plt.close()
2. PCA (Principal Component Analysis)
https://scikit-learn.org/dev/modules/generated/sklearn.decomposition.PCA.html
PCA는 말 그대로 주성분을 파악해 데이터의 분산구조를 잘 설명하는 "축"을 찾아내는 과정을 의미합니다. 이 또한 기존 데이터의 분포 특성을 최대한 보존하면서 축소하기 때문에 적은 차원을 데이터를 설명할 때 사용합니다.
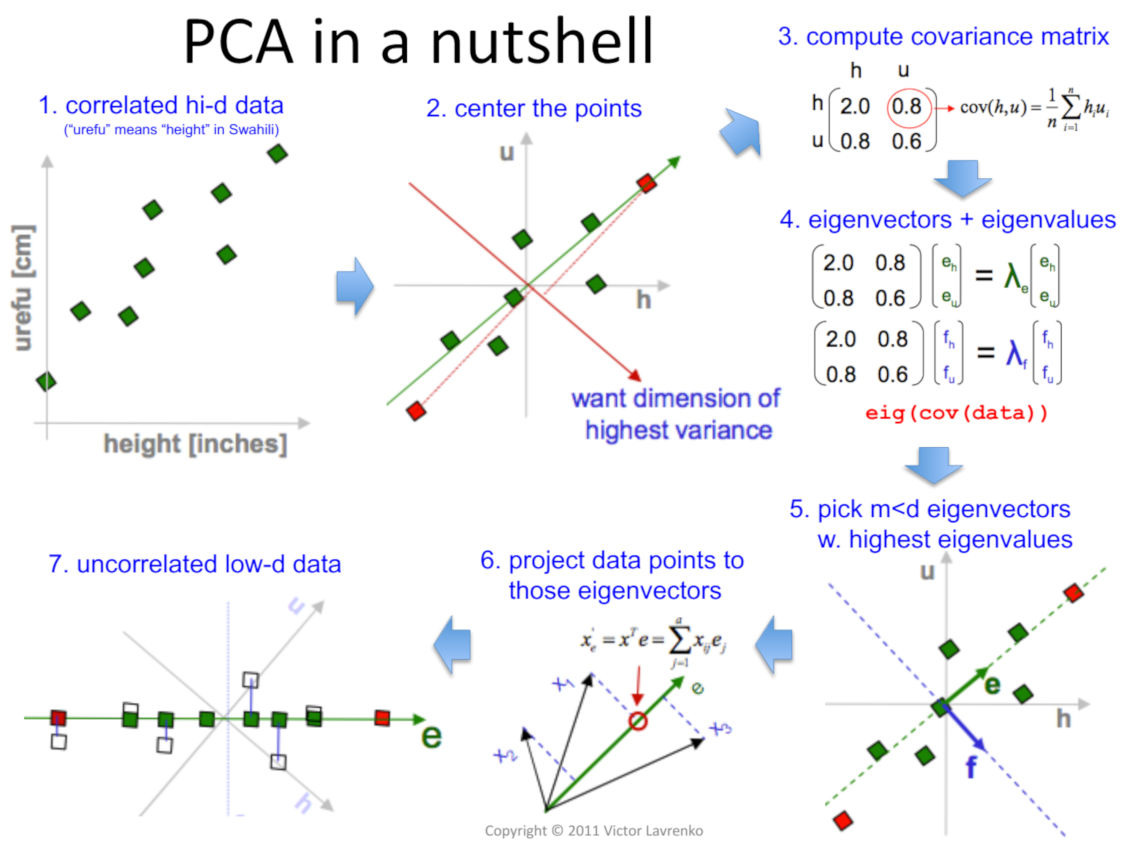
코드는 아래와 같습니다.
- real : [Data개수a, Embedding 차원]
- fake : [Data개수b, Embedding 차원]
- real_radii : [Data개수a], real 데이터에 대해 k번째 neighbours들과의 거리를 측정합니다.
- density : real 데이터의 k번째 neighbours와의 거리(real_radii)가 두 데이터 간의 거리(distance_real_fake)보다 큰 것에 한해 데이터 별로 거리 합을 구하고, 평균을 통해 밀도(겹치는 부분에 대한 정도)를 구해냅니다.
- distance_real_fake : [Data개수a, Data개수b], 각 데이터의 embedding간의 euclidean 거리를 측정합니다.
- coverage : real 데이터의 k번째 neighbours와의 거리(real_radii)가 두 데이터 간의 거리(distance_real_fake)중 제일 작은 것보다 큰 것에 한해, coverage(어느 정도 데이터 비율로 겹치는지)를 구해냅니다.
- real_2d : [Data개수a, 2]
- fake_2d : [Data개수b, 2]
from prdc import prdc
from sklearn.decomposition import PCA
def compute_density_coverage(real, fake, nearest_k):
distance_real_fake = prdc.compute_pairwise_distance(real, fake)
real_radii = prdc.compute_nearest_neighbour_distances(real, nearest_k)
density = (1.0 / float(nearest_k)) * (
distance_real_fake < np.expand_dims(real_radii, axis=1)
).sum(axis=0).mean()
coverage = (distance_real_fake.min(axis=1) < real_radii).mean()
pca = PCA(n_components=2)
real_2d = pca.fit_transform(real)
fake_2d = pca.transform(fake)
return real_radii, density, coverage, real_2d, fake_2d
그럼 이를 실행해 보겠습니다.
n_neighbors = min(len(a), len(b), 2)
real_radii, density, coverage, real_2d, fake_2d = compute_density_coverage(a,b,n_neighbors)
이렇게 만들어진 2D embedding을 plot해보겠습니다. 두 데이터를 보이는 것에 더해 추가적으로 plt.Circle()을 통해 real 데이터 포인트 들의 각 coverage 범위가 어떤가도 표시했습니다.
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 8))
plt.scatter(real_2d[:, 0], real_2d[:, 1], c='blue', label='Real', alpha=0.6)
plt.scatter(fake_2d[:, 0], fake_2d[:, 1], c='red', label='Fake', alpha=0.6)
for i in range(len(real_2d)):
circle = plt.Circle((real_2d[i, 0], real_2d[i, 1]), real_radii[i],
color='blue', fill=False, alpha=0.2)
plt.gca().add_artist(circle)
plt.title(f'Density: {density:.4f}, Coverage: {coverage:.4f}')
plt.xlabel('PCA Component 1')
plt.ylabel('PCA Component 2')
plt.legend()
plt.savefig('output.png')
plt.show()
#plt.close()
3. UMAP(Uniform Manifold Approximation and Projection)
UMAP은 데이터들에서 그래프를 구성하고, 각각의 node에서 정해진 radius의 원형을 그리고 겹치는 부분 "Strength"를 활용해 저차원으로 축소하는 알고리즘입니다. 빠르고 embedding차원 크기에 대한 제한도 없는데다가 global structure를 잘 보존하기 때문에 좋은 성능의 알고리즘으로 알려져 있습니다.

UMAP을 구현하는데 있어 필요한 패키지를 먼저 설치해줍니다.
pip3 install umap-learn==0.5.2
코드는 아래와 같습니다.
- real : [Data개수a, Embedding 차원]
- fake : [Data개수b, Embedding 차원]
- real_scaled : [Data개수a, Embedding 차원]
- fake_scaled : [Data개수b, Embedding 차원]
- real_umap :[Data개수a, 2]
- fake_umap : [Data개수b, 2]
from sklearn.preprocessing import StandardScaler
from umap import UMAP
def umap(real, fake):
scaler = StandardScaler()
real_scaled = scaler.fit_transform(real)
fake_scaled = scaler.fit_transform(fake)
umap_model=UMAP()
real_umap = umap_model.fit_transform(real_scaled)
fake_umap = umap_model.fit_transform(fake_scaled)
return real_umap, fake_umap
그럼 이를 실행해 보겠습니다.
real_2d, fake_2d = umap(a,b)
이렇게 만들어진 2D embedding을 plot해보겠습니다.
import matplotlib.pyplot as plt
plt.figure(figsize=(10, 8))
plt.scatter(real_2d[:, 0], real_2d[:, 1], c='blue', label='Real', alpha=0.6)
plt.scatter(fake_2d[:, 0], fake_2d[:, 1], c='red', label='Fake', alpha=0.6)
plt.title('Visualized embeddings')
plt.xlabel('UMAP Component 1')
plt.ylabel('UMAP Component 2')
plt.legend()
plt.savefig('output.png')
plt.show()
#plt.close()
https://github.com/SonyCSLParis/audio-metrics/blob/main/src/audio_metrics/density_coverage.py
'Developers 공간 [Shorts] > Vision & Audio' 카테고리의 다른 글
| [Generative] Llama 활용해 이미지에 대한 captioning, tagging하기 (2) | 2024.12.27 |
|---|---|
| [Generative] Huggingface 데이터 받아 사용하기 (0) | 2024.12.12 |
| [Generative] Python으로 FID 구하기 (0) | 2024.10.15 |
| [Audio] Python Pedalboard를 활용해 Audio를 바꾸기 (2) | 2024.10.10 |
| [Audio] Python활용해 BPM 측정하기 (0) | 2024.08.08 |
