2022. 12. 21. 00:53ㆍDevelopers 공간 [Basic]/Vision & Audio
Image Processing, Computer Graphics, Computer Vision은 항상 개념이 헷갈리기도 합니다.
먼저, Image Processing은 2차원 이미지을 가공하는 방법으로 Computer Vision의 일부분이라고 할 수 있습니다. 또한 Computer Graphics는 3차원 공간상의 정보를 2차원으로 rendering하여 보여주는 것을 의미하며, 뒤에서 설명할 Computer Vision의 반대라고 볼 수 있습니다.
마지막으로 Computer Vision는 2차원 및 3차원 이미지에서 다양한 정보 및 3차원 정보를 얻어내는 것을 의미합니다. 이는 말그대로 컴퓨터의 눈을 뇌에서 해석하는 과정을 의미합니다. Computer Vision을 위해서는 Calibration이라는 과정이 필요하기도 합니다.

이번 글에서는 Computer Vision과 Calibration에서 필요했던 개념에 대해서 정리하고자 합니다.
전문적인 글보다는 아는 정보를 정리한 글이니 내용 중에 더 자세히 알고 싶으시면 참조를 통해 자세한 글을 참조하시기 바랍니다.
<구성>
1. 카메라와 좌표계
a. 카메라의 종류
b. 좌표계와 파라미터
c. Calibration
2. Projection
a. Extrinsic Parameter를 활용한 변환
b. Intrinsic Parameter를 활용한 변환
c. 정리
3. Reconstruction
a. Bird's Eye View(BEV)
b. Depth Estimation 이해
c. Stereo Vision
d. Ego의 Motion을 활용한 방법
e. Scene Flow & Optical Flow
글효과 분류1 : 코드
글효과 분류2 : 폴더/파일
글효과 분류3 : 용어설명
글효과 분류4 : 글 내 참조
1. 카메라와 좌표계
카메라에는 핀홀 카메라와 Fisheye카메라가 있습니다. 이에 대한 간단한 설명 후에 카메라 모듈의 내부적인 구성에 대해 살펴보겠습니다. 또한, Logical한 좌표계의 종류와 그 사이 변환에 필요한 파라미터에 대한 개념에 대해서 먼저 살펴보겠습니다.
a. 카메라의 종류

- Fisheye 카메라와 Pinhole 카메라의 차이
- Pinhole 카메라 : 일반적으로 사용되는 카메라 모델이며, 직진으로 들어오는 lay를 normalized image plane으로 프로젝션한 후, image 좌표계로 변환하는 모델입니다.
- Fisheye 카메라 : 렌즈가 볼록하게 물고기 눈 모양을 하고 있어, 넓은 FOV를 가집니다. 핀홀 카메라와는 다르게 렌즈의 왜곡에 의해 빛이 꺾여 image plane에 프로젝션하는 모델입니다.
** FOV(Field Of View) 혹은 AOV(Angle Of View) : 좌우/상하 화각 또는 시야

- 카메라의 구성
- Image Sensor : CCD(Charge-Coupled Device) 센서 와 CMOS 센서가 있습니다. Image Sensor와 관련된 구성과 특징은 아래와 같습니다.
- Bayer Pattern : 인간의 시각 특성과 같이 RGGB 형태로 전통적인 CMOS, CCD 이미지 센서에서 배치하는 패턴입니다
- ISO : 사진을 찍었을 때 받아들인 빛 신호를 조절 하는 것으로, 높을수록 빛에 민감해 어두운 곳에서 촬영이 가능합니다.
- 셔터스피드 : 셔터가 열렸다 닫히는 시간으로 사진의 밝기에 영향을 줍니다.
- 셔터방식 : 롤링셔터방식과 글로벌셔터 방식이 있으며, 아래 그림을 보시면 알 수 있습니다.
- 롤링셔터방식 : 라인별 순차적으로 촬영하기 때문에 움직이는 물체를 촬영할 때 직선이 휘어있거나 진동 있는 직선은 지렁이처럼 꼬불꼬불 나오며, 가격이 저렴합니다.
- 글로벌셔터 : 움직일 때 찍어도 틀어지지 않는 특징을 가집니다.
- LFM(LED flicker mitigation) : 깜박임(flicker)이 있는 LED(Light Emitting Diode) 조명에서도 대상물을 정확히 인식하여 고품질의 영상을 얻는 것
- HDR(High Dynamic Range) : 명암(화면의 밝고 어두운 정도)의 범위를 넓혀, 밝은 부분은 더 밝고 세밀하게 보여주고, 어두운 부분은 더 어둡게 표현하되 사물이 또렷하게 보이도록 하는 이미지 표현 기술
- ISP(Image Signal Processor) : YUV 혹은 sRGB등 인간이 볼 수 있는 디지털로 변환하는 장치입니다. 카메라 모듈 중 ISP가 포함되어있는 경우도 있고, 없는 경우도 있습니다.
- Camera Module에 ISP가 없는 경우 frame grabber에 ISP를 포함시키는 경우도 있습니다.
** Frame Grabber :아날로그 신호를 디지털로 바꾸어 PC가 처리할 수 있도록 하는 ASIC/FPGA 보드를 뜻합니다. 위 구조의 경우 Deserializer가 Frame Grabber에 포함될 수 있습니다. - 최근엔 Image Sensor 자체에 ISP까지 포함된 경우도 있습니다.
- Camera Module에 ISP가 없는 경우 frame grabber에 ISP를 포함시키는 경우도 있습니다.
- SerDes(서데스) : Serializer와 Deserializer 를 합쳐 SerDes(서데스)라고 부르기도 합니다.
- 문제 상황을 예로 들어 아래 조건이 필요한 경우, 이를 위해 2,985,984,000bps가 필요합니다.
- FHD : 49,766,400 bits/frame(1080 x 1920 x 3 colors/pixel)
- 60fps
- video 시스템에서 데이터 전송을 최적화하기 위해 GMSL(Gigabit Multimedia Serial Link)가 필요했고, 이를 구현하는 방법이 Serializer와 Deserializer입니다.
** Serializer : pixel을 받아 serial bit stream으로 바꿔 Coax 혹은 shielded twisted pair로 전송합니다.
** Deserializer : serial bit stream을 decode해 복원된 video sync data를 전송합니다.
- 문제 상황을 예로 들어 아래 조건이 필요한 경우, 이를 위해 2,985,984,000bps가 필요합니다.
- Image Sensor : CCD(Charge-Coupled Device) 센서 와 CMOS 센서가 있습니다. Image Sensor와 관련된 구성과 특징은 아래와 같습니다.

b. 좌표계와 파라미터
카메라에서 사진을 찍을 때 알아야할 좌표계와 좌표계 간의 편환을 위한 파라미터를 먼저 살펴보고자 합니다.

- 좌표계 (Coordinate)
- World 좌표계 : 자동차를 예로, World 좌표계는 카메라가 장착되는 물체의 절대적인 좌표계를 의미하며, 오른손 법칙을 따릅니다.
- Camera 좌표계 : 자동차를 예로, Camera 좌표계는 카메라 자체의 좌표계를 의미하며, 오른손 법칙을 따릅니다.
- Image Plane : 이미지에서의 2D 좌표계를 의미하며, 보통 focal length를 1이라고 보는 Normalized plane과 그렇지 않은 Unnormalized plane이 있습니다.

- 카메라 파라미터
- Intrinsic Parameter : 카메라 내부 파라미터로, 카메라 제작과 관련있으며 카메라의 위치가 변해도 계속 쓸 수 있습니다. 이는 Camera좌표계와 Image Plane 간의 변환에 사용합니다.
- 3가지로 구성 됩니다.
- A. Focal Length : 초점의 길이 f_{x}, f_{y}
- B. Optical Center(Principal Points) : 광점의 위치 c_{x}, c_{y}
- C. Skew Factor : 휘어짐 정도를 의미하는 파라미터 skew_c 혹은 tan(α) 며, 아래 그림을 참조하세요.
- 구성 : 위의 파라미터를 모두 포함해 3x3 Matrix로 구성합니다.
\begin{pmatrix} f_{x} & skew & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \\ \end{pmatrix}
- 3가지로 구성 됩니다.
- Extrinsic Parameter : 외부요소 파라미터로, World 좌표계와 Camera 좌표계 간의 변환에 사용합니다. 카메라의 위치나 상태가 변하면 다시 구해야 합니다.
- 2가지로 구성 됩니다. :
- A. Rotation(R) : yaw,pitch, roll을 포함해 3차원 회전 변환 행렬을 의미합니다.
**주의 : 좌표계의 Rotation과 좌표의 Rotation은 반대 방향입니다. (보통 좌표 기준)
**참조 : Rotation의 Inverse는 행렬의 transpose와 같습니다. 이는 Rotation Matrix가 Orthogonal Matrix(직교행렬)이기 때문입니다. - B. Translation(T) : x,y,z좌표로 좌표계를 이동시키기 위한 이동값을 의미합니다.
**주의 : Rotation 적용 이전의 이동인지, 적용 이후의 이동인지에 따라 x,y,z가 기준이 다릅니다. (보통 이후 기준)
**참조 : (적용 이후인 경우) Translation의 Inverse는 반대방향으로 가는 Rotation을 곱한 뒤, (-) 값을 해주면 됩니다.
- A. Rotation(R) : yaw,pitch, roll을 포함해 3차원 회전 변환 행렬을 의미합니다.
- 구성 : 위 R,T를 합쳐서 3x4 Matrix 형태로 구성합니다.
- 2가지로 구성 됩니다. :
- Intrinsic Parameter : 카메라 내부 파라미터로, 카메라 제작과 관련있으며 카메라의 위치가 변해도 계속 쓸 수 있습니다. 이는 Camera좌표계와 Image Plane 간의 변환에 사용합니다.
\begin{bmatrix} R|t\end{bmatrix}=\begin{bmatrix}r_{00} & r_{01} & r_{02} & t_0 \\r_{10} & r_{11} & r_{12} & t_1 \\r_{20} & r_{21} & r_{22} & t_2 \\ \end{bmatrix}
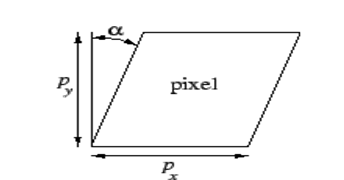
c. Calibration
위의 파라미터들을 얻는 과정을 Calibration이라고 합니다.
먼저 Intrinsic Parameter fx,fy,cx,cy, skew의 경우 카메라 제조시 물리적으로 제공되는 값이 있고, 실제 camera 결과 값을 보며 구해내는 값이 있습니다. 실험을 통해 알아내는 경우, 2D 체스보드(정4각형이 포함된)를 촬영한 이미지를 통해 pixel 단위로 focal length 와 cx,cy를 알아내기도 합니다.
2D체스보드와 함께 Calibration하는 코드는 아래와 같습니다. 아래는 이미지 한장에 대한 코드이지만, 여러개의 사진에 대해 진행해야합니다.
// STEP1. Prepare==================================== Mat img = cv2::imread('/PATH/TO/abc.png'); Mat img_gray; cv::cvtColor(img, img_gray, cv::COLOR_BGR2GRAY); // CHECKERBOARD : 28mm square(6x9) vector<cv::Point3f> worldpoints; for(int i=0; i<6;i++){ for(int i2=0; i2<9;i2++){ // z(0.0mm), 28mmx28mm worldpoints.push_back(cv::Point3f(i2*28,i*28,0)); } } // STEP2. Get Corners==================================== vector<cv::Point2f> corners; bool found = cv::findChessboardCorners(img_gray, cv::Size(9,6), corners, CV_CALIB_CB_ADAPTIVE_THRESH|CV_CALIB_CB_FAST_CHECK|CV_CALIB_CB_NORMALIZE_IMAGE); drawChessboardCorners(img, cv::Size(9,6), corners, found); imshow("Check Corners in image", img); waitKey(30); // refine pixel coords for given 2d points cv::TermCriteria criteria(CV_TERMCRIT_ITER | CV_TERMCRIT_EPS, 100, 0.001); cornerSubPix(img_gray, corners, Size(11,11), Size(-1,-1), criteria); vector<vector<cv::Point3f> > objectPoints; vector<vector<cv::Point2f> > imagePoints; imagePoints.push_back(corners); objectPoints.push_back(worlpoints); cv::destroyAllWindows(); // STEP3. Calibration========================================= Mat cameraMatrix = Mat::eye(3,3,CV_64F); Mat distCoeffs = Mat::zeros(5,1,CV_64F); vector<Mat> rvecs, tvecs; double rms = calibrateCamera(objectPoints, imagePoints, cv::Size(img_gray.rows, img_gray.cols), cameraMatrix, distCoeffs, rvecs, tvecs, CV_CALIB_FIX_K4 | CV_CALIB_FIX_K5, TermCriteria(CV_TERMCRIT_ITER + CV_TERMCRIT_EPS, 200, 1e-5) ); cout << "rms:" << rms << endl;
다음으로 Extrinsic Parameter의 경우 보통 아래 그림과 같이 거리 값을 알 수 있는 좌표를 배치 시켜 여러 장 찍어서 calibration합니다. 이때 코드는 아래와 같습니다.

#include <opencv2/opencv.hpp> using namespace std; using namespace cv; vector<Point3f> worldPoints; vector<Point2f> imagePoints; // Intrinsic-Input // (fx, 0, cx) (0, fy, cy) (0, 0, 1) Mat cameraMatrix = Mat_<double>(3,3, CV_64F, Scalar()); // k1, k2, p1, p2, [,k3] Mat distCoeffs = Mat_<double>(5,1); // Extrinsic-Output Mat rvec = Mat_<double>(3,1); // (Rx, Ry, Rz) Mat tvec = Mat_<double>(3,1); // (Tx, Ty, Tz) solvePnP(worldPoints, imagePoints, cameraMatrix, distCoefffs, rvec, tvec); // Rotation Matrix (World->Camera) Mat R Rodrigues(rvec, R);
2. Projection
필요한 파라미터들을 알아내는 과정을 Calibration이라고 하며, 앞에서 이를 알아보는 과정을 알아보았습니다.
이제 그 Calibration 파라미터를 알고 있다는 전제하에 Image좌표계로 Projection하는 과정에 대해서 알아보고자 합니다. 전체적으로 World 좌표계에서 Image좌표계로 바꾸는 식은 아래와 같습니다.
A\begin{bmatrix} R|t\end{bmatrix}\begin{bmatrix} X \\ Y \\ Z \\ 1 \\ \end{bmatrix} = \begin{bmatrix}f_x & skew*f_x & c_x \\0 & f_y & c_y \\0 & 0 & 1 \\\end{bmatrix}\begin{bmatrix}r_{00} & r_{01} & r_{02} & t_0 \\r_{10} & r_{11} & r_{12} & t_1 \\r_{20} & r_{21} & r_{22} & t_2 \\\end{bmatrix}\begin{bmatrix}X \\ Y \\ Z \\ 1 \\\end{bmatrix} = s\begin{bmatrix}x \\ y \\ z \\\end{bmatrix}
위 과정에 distortion을 반영하는 내용은 없습니다. 실제로는 렌즈의 비선형성에 의해서 왜곡이 발생하는데 이를 반영하면 뒤에서 코드가 달라집니다. distortion을 반영하지 않았을 때, 위식을 표현한 코드는 아래와 같습니다.
이전 챕터 Calibration을 통해 얻는 Rotation과 Translation은 "World좌표계에서 Camera좌표계로"의 값이고, 이로부터 시작하겠습니다.
** 혹시나 "Camera좌표계에서 World좌표계로"의 값이 필요하다면, Rotation은 inverse를 해주고 Translation은 반대방향으로 가는 Rotation을 곱한 뒤, (-) 값을 해주면 이 됩니다.
- Mat new_R = Mat_(3,3);
Mat new_T = Mat_(3,1);
Rodrigues(-rvec,new_R); // -rvec : camera -> world
new_T= new_R * -tvec; // -(R*tvec) : camera -> world
#include <opencv2/opencv.hpp> using namespace cv; using namespace std; int main(){ // Extrinsic & Intrinsic Parameters - Input Mat rvec = Mat_<double>(3,1); Mat tvec = Mat_<double>(3,1); Mat cameraMatrix = Mat_<double>(3,3); // Prepare for Rotation Mat R = Mat_<double>(3,3); // World -> Camera Rodrigues(rvec, R); // World -> Camera Mat P = Mat_<double>(3,4); hconcat(R,tvec,P); // World -------> Image Mat temp = cameraMatrix*P; //(3,4) Mat worldPoint = (Mat_<double>(4,1) << 9999999.0, 0.0, 0.0, 1.0); Mat vanishingPoint = temp*worldPoint; // (3,1) vanishingPoint = vanishingPoint/vanishingPoint.at<double>(2,0); // Image --------World Mat PnoZ = (Mat_<double>(3,3) << P.at<double>(0,0), P.at<double>(0,1), P.at<double>(0,3),\ P.at<double>(1,0), P.at<double>(1,1), P.at<double>(1,3),\ P.at<double>(2,0), P.at<double>(2,1), P.at<double>(2,3)); Mat newtemp = cameraMatrix*PnoZ; //Size(3,3) Mat inversePnoZ = newtemp/newtemp.at<double>(2,2); //Size(3,3) inversePnoZ = inversePnoZ.inv(); //Size(3,3) Mat imagePoint = (Mat_<double>(3,1) << 1000,500, 1.0); Mat world = inversePnoZ * imagePoint; //Size(3,1) }
a. Extrinsic Parameter를 활용한 변환
먼저 World 좌표계에서 Camera 좌표계로 Translation, Roation을 활용해 이동하는 과정에 대해 살펴보려고 합니다.
먼저 식은 아래와 같습니다. Rotation과 Translation을 합친 3x4 matrix와 곱하는 것과 3x3 Rotation을 곱한 이후에 3x1 Translation을 "더하는" 것은 같습니다.
\begin{bmatrix} R|t\end{bmatrix}\begin{bmatrix} X \\ Y \\ Z \\ 1 \\ \end{bmatrix} = \begin{bmatrix}r_{00} & r_{01} & r_{02} & t_0 \\r_{10} & r_{11} & r_{12} & t_1 \\r_{20} & r_{21} & r_{22} & t_2 \\\end{bmatrix}\begin{bmatrix}X \\ Y \\ Z \\ 1 \\\end{bmatrix} = RX+T = \begin{bmatrix}r_{00} & r_{01} & r_{02} \\r_{10} & r_{11} & r_{12} \\r_{20} & r_{21} & r_{22} \\\end{bmatrix}\begin{bmatrix}X \\ Y \\ Z \\ \end{bmatrix} + \begin{bmatrix}t_0 \\ t_1 \\ t_2\\ \end{bmatrix}
이미 위에서 다 설명되었지만 world좌표계의 point를 camera좌표계의 point로 옮겨주는 코드는 아래와 같습니다. 단순히 Matrix를 만들어 곱하는 것입니다.
#include <opencv2/opencv.hpp> using namespace cv; using namespace std; int main(){ // Extrinsic & Intrinsic Parameters - Input Mat rvec = Mat_<double>(3,1); Mat tvec = Mat_<double>(3,1); Mat cameraMatrix = Mat_<double>(3,3); // Prepare for Rotation Mat R = Mat_<double>(3,3); // World -> Camera Rodrigues(rvec, R); // World -> Camera Mat P = Mat_<double>(3,4); hconcat(R,tvec,P); // World -------> Camera Mat worldPoint = (Mat_<double>(4,1) << 9999999, 0.0, 0.0, 1.0); Mat cameraPoint = P * worldPoint; // (3,1) }
- Matrix Decomposition
위에서 Calibration에서 보셨다시피 3x3 rotation matrix가 가장 먼저 구해지기 때문에, Yaw, Pitch, Roll을 알고 싶은 경우 아래와 같이 Matrix Decomposition 하여 알아 낼 수 있습니다. 하지만 회전 순서에 따라 (XYZ, ZXY, ZXZ, XYX, YXY, YZY, ZYZ, ZXZ, XZY, YXZ, YZX, ZYX)와 같이 12개의 서로 다른 표현법이 가능하고 Decomposition 하는 방법에 따라서 yaw, pitch, roll 값이 달라집니다.
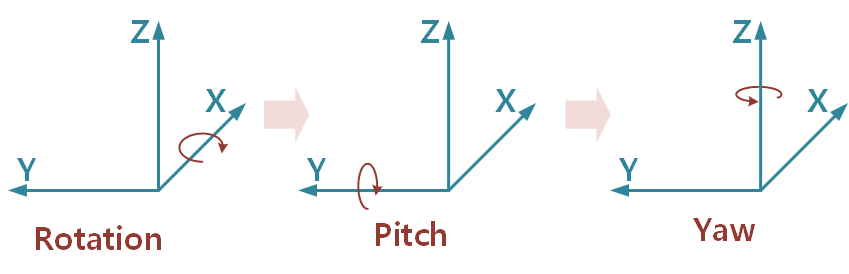
그 중에 아래 식은 아래 그림과 같이 Rotation을 적용하고, Pitch를 적용하고, Yaw를 적용하는 순서대로 작동하는 식입니다. 방향은 오른나사 법칙을 따릅니다.
\begin{bmatrix} cos(yaw) & -sin(yaw) & 0 \\ sin(yaw) & cos(yaw) & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} cos(Pit) & 0 & sin(Pit) \\ 0 & 1 & 0 \\ -sin(Pit) & 0 & cos(Pit) \\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos(Rot) & -sin(Rot) \\ 0 & sin(Rot) & cos(Rot) \\ \end{bmatrix}\begin{bmatrix} X_{w} \\ Y_{w} \\ Z_{w} \\ \end{bmatrix} = \begin{bmatrix} X_{c} \\ Y_{c} \\ Z_{c} \\ \end{bmatrix}

위와 같은 순서로 decomposition을 할 때의 yaw, pitch, roll 을 구하는 방법은 아래와 같습니다. 아래와 같은 Rotation Matrix가 있을 때 x축 기준 회전(Rotation), Y축 기준 회전(Pitch), Z축 기준 회전(Yaw)는 각각 아래와 같습니다.
\begin{bmatrix}r_{00} & r_{01} & r_{02} \\ r_{10} & r_{11} & r_{12} \\ r_{20} & r_{21} & r_{22} \\\end{bmatrix}
\Theta_{x} = atan2(r_{21}, r_{22})
\Theta_{y} = atan2(-r_{20},\sqrt{r_{21}^{2}+r_{22}^{2}})
\Theta_{z} = atan2(r_{10}, r_{00})
다음은 위를 기반으로 오일러 각도(Euler Angle)를 얻어내는 코드입니다.
** 오일러 각도(Euler Angle) : 고정된 축으로 회전하는 Fixed Angle과 다르게, 회전한 축을 기준으로 다음 회전을 합니다.
#include “stdlib.h” #include “stdio.h” #include “string.h” #include <opencv2/opencv.hpp> #include <jsoncpp/json/json.h> using namespace std; using namespace cv; vector<double> split(string input, char delimeter){ vector<double> answer; stringstream ss(input); string temp; while(getline(ss,temp,delimeter)){ answer.push_back(stod(temp)); } return answer; } const float DEG2RAD=CV_PI/180.0; const float RAD2DEG=180.0/CV_PI; int main(){ string ROOT_PATH = "./"; char file_name[100]; sprintf(file_name, "%s/Calibration.json", ROOT_PATH.c_str()); Json::Value root; Json::Reader reader; ifstream json(file_name, ifstream::binary); if(!json) printf("Error!\n"); const Json::Value extrinsic = root["Extrinsic"]; if(!extrinsic['name'].asString().compare('MyName')){ char delimeter = ','; vector<double> tempout = split(extrinsic['value'].asString().delimeter); Mat rotationMatrix = Mat_<double>(3,3); for(int row=0;row<3;row++){ for(int col=0;col<3;col++){ rotationMatrix.at<double>(row,col) = tempout[row*3+col]; } } double theta_x = atan2(rotationMatrix.at<double>(2,1), rotationMatrix.at<double>(2,2)) * RAD2DEG; double theta_y = atan2(rotationMatrix.at<double>(2,0), sqrt(pow(rotationMatrix.at<double>(2,1),2)+pow(rotationMatrix.at<double>(2,2),2))) * RAD2DEG; double theta_z = atan2(rotationMatrix.at<double>(1,0), rotationMatrix.at<double>(0,0)) * RAD2DEG; } }
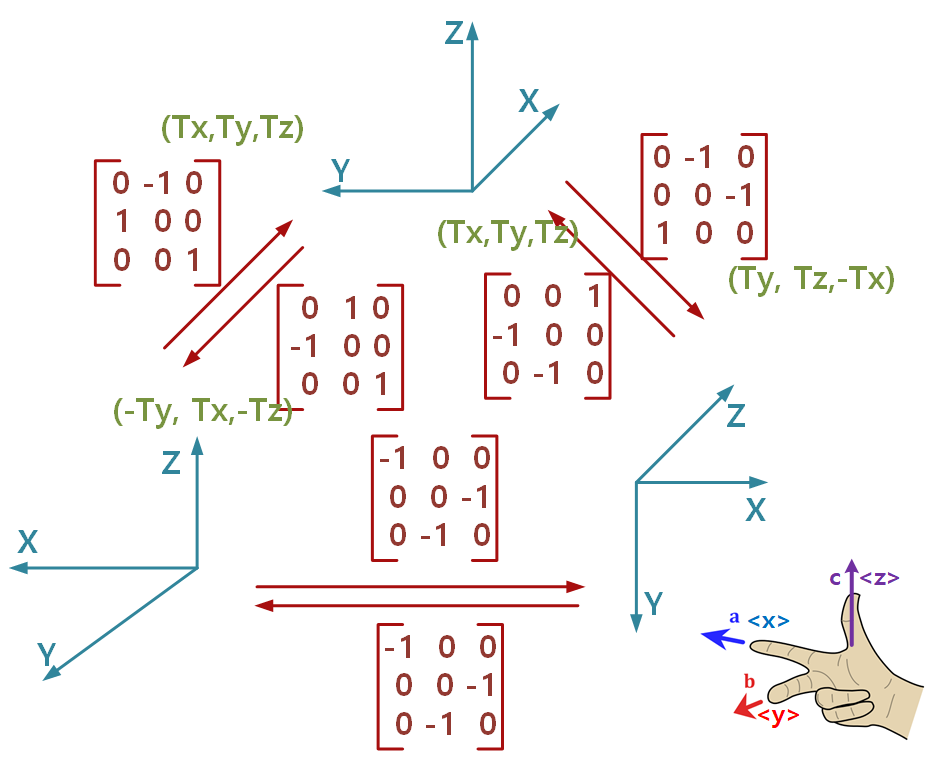
- 사실 Rotation Matrix는 3차원 변환 Matrix에 대해 이해하면 편합니다. 아래는 예로 몇 개의 좌표계 간의 변환시 Unit Matrix 변환식을 나타낸 것입니다. 좌표계는 당연히 오른손 법칙을 따릅니다. 확인할 수 있는 여러가지 특징을 정리해 놓습니다.
- Rotation 주의 : 좌표 기준의 Matrix 입니다.
- Rotation 참조 : 반대 방향의 Rotation은 행렬의 Transpose입니다.
- Translation 주의 : Rotation 적용 이후에 적용하는 Translation입니다.
- Translation 참조 : 반대방향의 Translation은 "왼쪽 아래"에서 "위"로 이동한 Translation (Tx,Ty,Tz)은 "위"의 좌표계 기준 x,y,z이므로, 반대방향의 Translation은 반대방향 [0,1,0 | -1,0,0 | 0,0,1]을 곱해준 뒤 (-)를 해준 (-Ty,Tx,-Tz)입니다.
b. Intrinsic Parameter를 활용한 변환
이번엔 Intrinsic 파라미터를 활용해 Camera 좌표계의 값들을 Image 좌표계로 옮기는 작업에 대해 살펴보려고 합니다. 이 과정은 frustum(절두체)에서 Image로 차원을 줄여주는 undistortion 과정으로, 카메라 좌표계의 Z 값이 사라지므로 비가역적인 과정이라고 볼 수 있습니다.
아래는 먼저 Z 축을 기준으로 Normalize하는 과정입니다.
\begin{bmatrix} X_{c}/Z_{c} \\ Y_{c}/Z_{c} \\ \end{bmatrix} = \begin{bmatrix} x_{u} \\ y_{u} \\ \end{bmatrix}
이제 카메라에 적용된 distortion을 없애는 작업이 필요합니다. 위에 전체적인 과정에서는 포함되지 않았지만 실제로는 렌즈의 비선형성때문에 왜곡이 생깁니다. 식은 아래와 같은데, k1,k2는 radial distortion이라고 하고 p1,p2은 tangential distortion이라고 하고, 이때 사용하는 r_u는 왜곡이 없을 때 principal point까지의 반지름으로, 아래 자세히 설명합니다.
r_{u}^{2}=x_{u}^{2} + y_{u}^{2}
(1+k_{1}r_{u}^{2} + k_{2}r_{u}^{4})\begin{bmatrix} x_{u} \\ y_{u} \\ \end{bmatrix} + \begin{bmatrix} 2p_{1}x_{u}y_{u} + p_{2}(r_{u}^{2} + 2x_{u}^{2}) \\ p_{1}(r_{u}^{2} + 2y_{u}^{2}) + 2p_{2}x_{u}y_{u} \\ \end{bmatrix} = \begin{bmatrix} x_{n} \\ y_{n} \\ \end{bmatrix}
위 과정은 왜곡된 영상좌표로부터 왜곡 보정된 영상좌표를 구하는 과정으로, closed-form solution이 없는 매우 어려운 문제이기 때문에 보통 근사적으로 해를 구합니다. 따라서 x_u, y_u로부터 x_n, y_n을 구하는 것은 쉬우나 반대는 7차 방정식을 풀어야 하는 매우 어려운 문제입니다. 따라서 이 과정은 비가역적인 과정이라고 할 수 있습니다.
위에 대해 설명하려면 아래 그림에 대해 이해할 필요가 있습니다. 해당 그림은 하기 논문을 참조했습니다.
https://ieeexplore.ieee.org/document/1333993
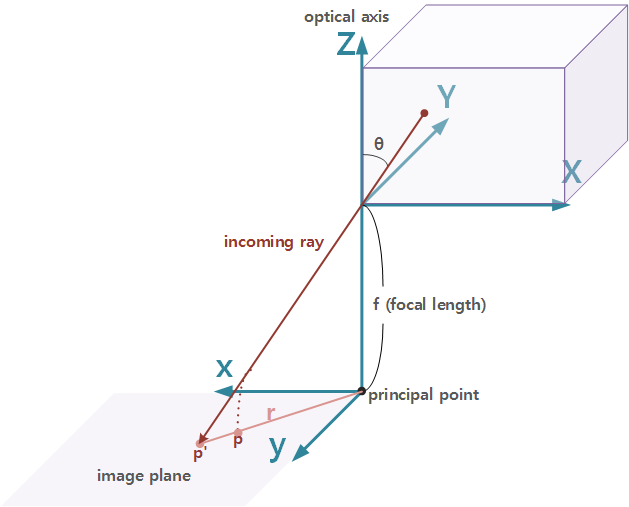
위에 incoming ray가 opticcal axis와 이루는 각도를 Θ라고 했을 때 밖의 점이 image plane에 맺히는 위치 p'과 p는 각각 pinhole 카메라 모델일 때의 image point와, fisheye 카메라 모델일 때의 image point입니다.
먼저 principal point로부터 pinhole camera 모델일 때의 p'까지의 거리인 r 은 f * tanΘ로 표현할 수 있습니다. 하지만 principal point로부터 fisheye camera 모델일 때의 p까지의 거리인 r 은 아래와 같이 여러가지 있습니다.
- stereographic projection : 2f * tanΘ
- equidistance projection : f * Θ
- equisolid angle projection : 2f * sinΘ
- orthogonal projection : f * sinΘ
이 중에 가장 흔한 것은 equidistance projection이며, 이들을 가장 general한 form으로 나타낸 것이 아래와 같은 form 입니다.
(개인적인 생각으로는 tan와 sin함수가 포함되어있으니 테일러 급수를 활용한 표현법을 활용한 것이지 않을까 싶습니다.)
결과적으로 아래와 같은 distortion식이 나오게 된 것입니다.
r(\Theta ) = k_{1}\Theta + k_{2}\Theta^{3}+ k_{3}\Theta^{5}+ k_{4}\Theta^{7} ...
왜곡이 사라진 (x_n, y_n)은 normalized image plane의 좌표입니다. 이제 마지막으로 위에서 했던것과 같이 intrinsic matrix를 곱해주면 픽셀로 표현되는 좌표계로 변환됩니다.
\begin{bmatrix}f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 0 \\ \end{bmatrix}\begin{bmatrix} x_{n} \\ y_{n} \\ 1 \end{bmatrix} = \begin{bmatrix} x_{p} \\ y_{p} \\ 1 \end{bmatrix}
아래는 이 과정을 코드로 구현한 결과입니다.
// Intrinsic Parameters - Input Mat cameraMatrix = Mat_<double>(3,3); Mat distCoeffs = Mat::zeros(5,1,CV_64F); // Prepare for Intrinsic Mat image; Mat mapX, mapY; initUndistortRectifyMap(cameraMatrix, distCoeffs, Mat(), newCameraMatrix, Size(image.cols,image.rows), CV_32FC1, mapX, mapY) // Remap with mapping Mat image_out; remap(image, image_out, mapX, mapY, CV_INTER_NN, BORDER_CONSTANT);
이렇게 Intrinsic Parameter를 활용해 Undistortion하는 과정을 Rectification이라고 부르는 사람들이 있습니다.
하지만 Rectification이라는 말은 실제로는 Stereo Matching에서 쓰이는 말로, Stereo 카메라의 장착사양을 두축은 동일하게 맞추기 위해 렌즈 왜곡을 보정하고 카메라간 거리만큼만 차이가 나도록 보정하는 과정입니다.
이 과정 자체가, affine transformation인 undistortion 과정을 포함하기 때문에 동일하게 쓰이기도 하는 것 같습니다.
**affine transformation : 이상적이지 않은 카메라 각도에서 발생하는 기하학적 왜곡이나 형태 변형을 보정하는 데 주로 사용되는 선형 매핑 방법

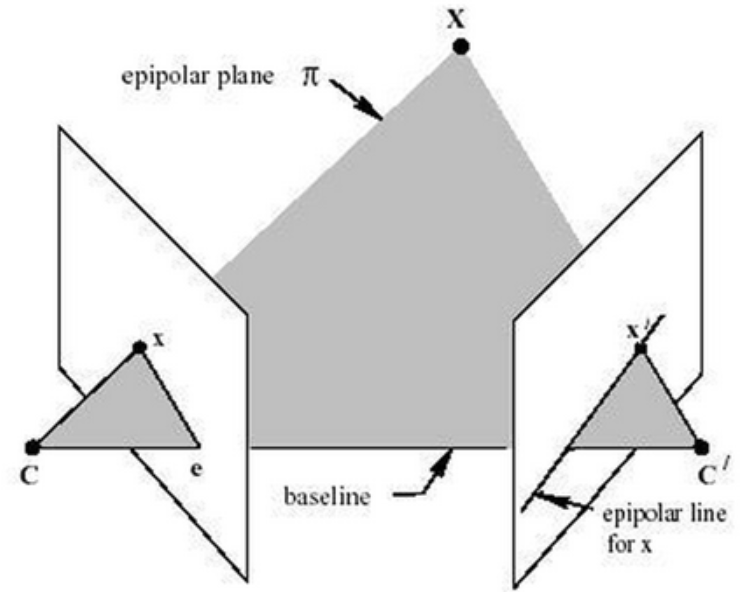
즉, Stereo Matching을 위한 Rectification 과정은 위 그림과 같이 Intrinsic을 활용해 이미지를 피는 undistortion 과정과 Extrinsic을 활용해 Align을 맞추는 과정이 있는데, undistortion이 포함되었기 때문에 이 과정을 "Rectify"라고도 하는 것이며, 사실 실제로는 위 그림과 같이 epipolar line을 맞추는 과정까지도 "Rectify"이라고 하는 것입니다.
또한 opencv에 있는 initUndistortRectifyMap()이라는 함수를 사용하기 때문에 Rectification이라는 말을 사용하는 것 같기도 합니다.
** Epipolar geometry : 스테레오 비전(stereo vision) 즉, 2-view 비전에서의 기하학으로 동일한 사물 또는 장면에 대한 영상을 서로 다른 두 지점에서 획득했을 때, 영상 A와 영상 B의 매칭쌍들 사이의 기하학적 관계입니다. 아래 그림에서 C와 C’은 두 개 각 카메라의 광원입니다.
c. 정리
이제 앞서 처음에 보인 것 과 다르게, distortion까지 반영해서 world 좌표계에서 이미지 plane으로 옮기는 과정의 코드는 아래와 같습니다.
distortion을 반영한 cameraMatrix를 얻어내는 방법에는 initUndistortRectifyMap() 함수를 사용하는 방식과 getOptimalNewCameraMatrix() 함수를 사용하는 방식이 있습니다. getOptimalNewCameraMatrix()에 들어가는 alpha값은 undistortion하고 나면 아래 그림과 같이 방사형태의 의미지가 되는데, 원본이미지의 크기를 유지하고 싶다면 alpha값을 0으로 주면되고, 까만색 padding부분을 포함하려면 1에 가깝게 주면됩니다.
참고로 이렇게 undistortion한 이후에 extrinsic parameter 중 rotation까지 반영해 수평형태로 만든 rectification한 결과를 활용하기도 합니다. rectification에 대해서는 앞의 챕터를 참조합니다.

#include <opencv2/opencv.hpp> using namespace cv; using namespace std; int main(){ // Extrinsic & Intrinsic Parameters - Input Mat rvec = Mat_<double>(3,1); Mat tvec = Mat_<double>(3,1); Mat cameraMatrix = Mat_<double>(3,3); Mat distCoeffs = Mat_<double>(5,1); // Prepare for Extrinsic Mat R = Mat_<double>(3,3); // World -> Camera Rodrigues(rvec, R); // World -> Camera Mat P = Mat_<double>(3,4); hconcat(R,tvec,P); // Prepare for Intrinsic Mat image; Mat newCameraMatrix; // Get New cameraMatrix with distortion - method1 initUndistortRectifyMap(cameraMatrix, distCoeffs, Mat(), newCameraMatrix, Size(image.cols,image.rows), CV_32FC1, mapX, mapY) // Get New cameraMatrix with distortion - method2 newCameraMatrix = getOptimalNewCameraMatrix(cameraMatrix, distCoeffs, Size(image.cols,image.rows), alpha, Size(image.cols,image.rows), 0, true); // World -------> Image Mat temp = cameraMatrix*P; //(3,4) Mat worldPoint = (Mat_<double>(4,1) << 9999999, 0.0, 0.0, 1.0); Mat vanishingPoint = temp*worldPoint; // (3,1) vanishingPoint = vanishingPoint/vanishingPoint.at<double>(2,0); }
3. Reconstruction
Computer Vision이란 Reconstruction이 핵심이기도 합니다. 즉 이미지에서 정보를 얻어내는 것이 Computer Vision의 핵심인데, 그 중 3D 정보를 얻기에는 world좌표계에서 이미지 plane으로 옮길 때, "깊이 값(혹은 카메라 좌표계에서의 Z값이라고도 합니다)"이 사라졌으므로 정확하게 얻기 힘들 것 같습니다. 이런 상황에서 어떻게 상황을 극복해 정보를 얻어 낼 수 있는지 살펴보도록 합니다.
a. Bird's Eye View(BEV)
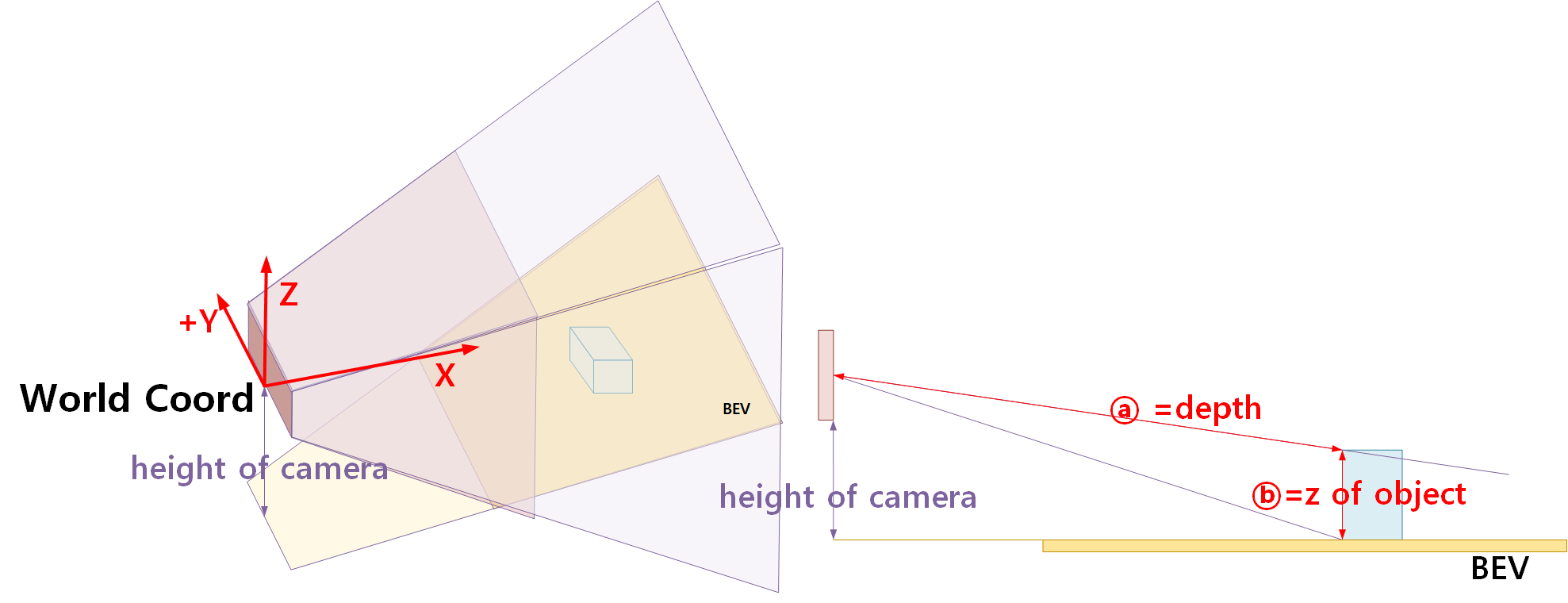
world 좌표계 기반으로 BEV를 얻어낸다면 이미지에 있는 모든 정보를 3D에 위치 시킬 수 있을 것입니다. 하지만 위 그림에서 ⓐ(Object까지의 Depth) 혹은 ⓑ(Object의 z)를 모르기 때문에 정확하게 3D 좌표계로 옮길 수 없습니다.
Object의 위치를 모르기 때문에 그냥 height of camera를 어떤 기준(주로 "지면 기준")을 가정하고, 해당 기준으로 하나의 평면으로 잘라서 BEV를 얻어내기도 합니다. 즉, BEV는 가정된 지면에 의한 2D 좌표값입니다.
그래서 Pseudo Lidar 혹은 Depth Estimation을 활용해 2D Image에서 필요한 3D 정보를 얻으려고 하는 논문이 필요한 것입니다.
아래는 BEV변환을 위한 코드입니다.
// Intrinsic Parameters - Input Mat cameraMatrix = Mat_<double>(3,3); Mat distCoeffs = Mat_<double>(5,1); // Prepare for Intrinsic Mat imageBefore; Mat newCameraMatrix; Mat mapX, mapY; initUndistortRectifyMap(cameraMatrix, distCoeffs, Mat(), newCameraMatrix, Size(imageBefore.cols,imageBefore.rows), CV_32FC1, mapX, mapY) // Homography Transformation // LeftTop, RightTop, LeftBottom, RightBottom vector<Point2f> CornerBefore = {Point2d(ax,ay),Point2d(bx,by),Point2d(cx,cy),Point2d(dx,dy)}; vector<Point2f> CornerAfter = {Point2d(Ax,Ay),Point2d(Bx,By),Point2d(Cx,Cy),Point2d(Dx,Dy)}; Mat transformation = getPerspectiveTransform(CornerBefore, CornerAfter); Size newSize(Bx-Ax+1,Cy-By+1); // Get "AfterImage" Mat imageAfter; warpPerspective(imageBefore, imageAfter, transformation, newSize, cv::BORDER_CONSTANT); // Get "AfterImage" with mapping + undistortion Mat mapAfterX, mapAfterY; warpPerspective(mapX, mapAfterX, transformation, newSize, cv::BORDER_CONSTANT); warpPerspective(mapY, mapAfterY, transformation, newSize, cv::BORDER_CONSTANT); remap(imageBefore, imageAfter, mapAfterX, mapAfterY, cv::CV_INTER_NN, cv::BORDER_CONSTANT);
b. Depth Estimation 이해
Depth Estimation이란 이미지 정보에서 Dense한 Depth 이미지를 얻어내는 방법입니다. 다양한 용어가 있는데 용어에 대해서는 아래 간단히 소개합니다.
- Disparity Map : Depth map을 얻기 위한 중간 feature입니다. 사실은 Disparity map은 Stereo 정합을 위한 두 이미지에서 같은 픽셀에 대해 다른 parallax 차이 값을 의미하는 데, 이 값과 depth의 관계를 통해 depth map을 얻어냅니다.
- Depth Map: World 좌표계에서의 추정된 Depth 매핑.
- Depth Completion : 라이다 등 sparse한 3D 정보가 이미 있을 때, 이를 기반으로 dense한 depth map을 만들어내는 과정.
- Depth Estimation : 아무 것도 없을 때 다양한 정보를 활용해 dense한 per-pixel 2D depth map을 만드는 과정.
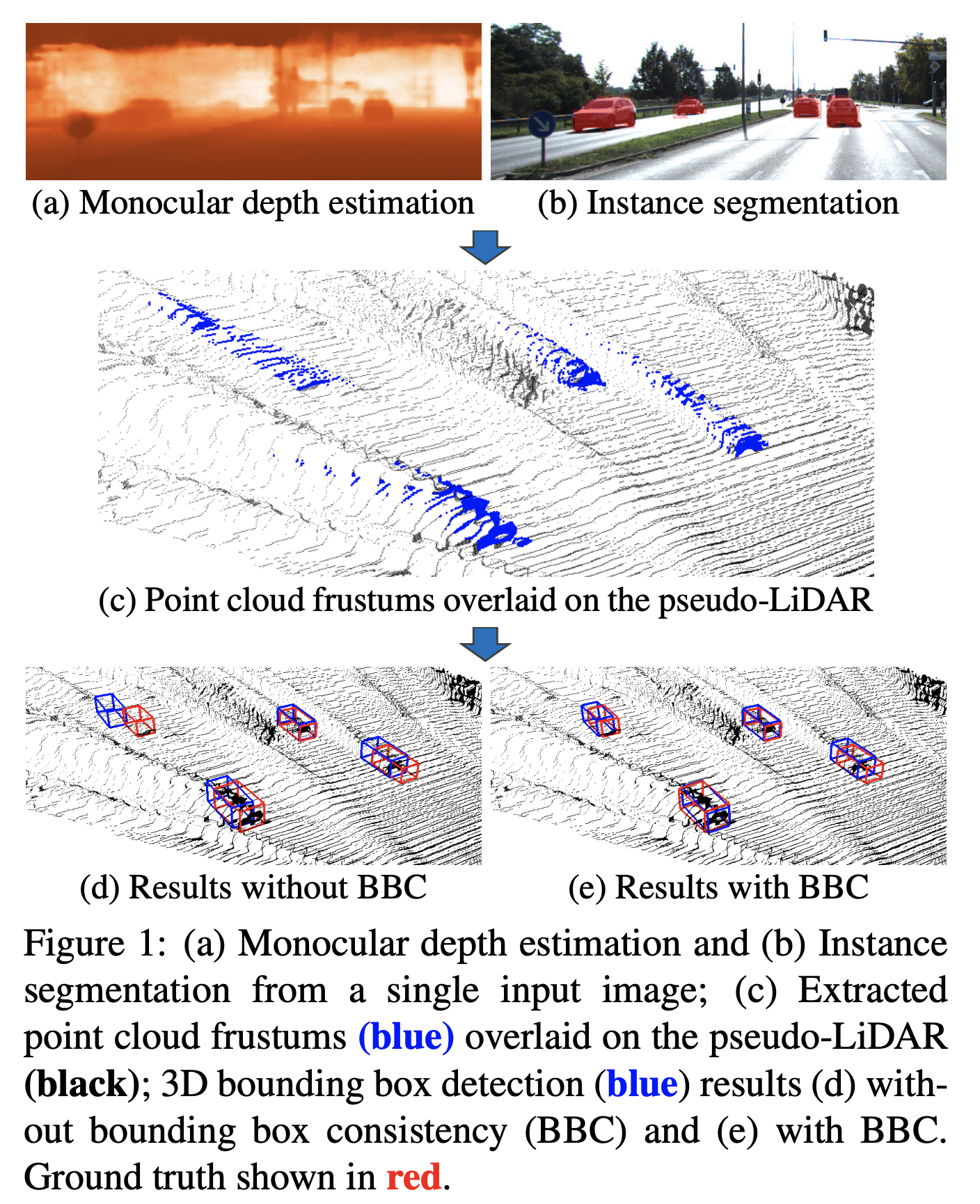
Depth Estimation에 대한 최신 논문과 트렌드는 파악하고 나서 이야기하는 것이 좋을 것 같아 깊게 다루지 않겠습니다. 하기 논문 하나만 소개하자면, 3D Object Detection을 위한 논문으로, 3D Object Detection에 있어서 3D BBox(Bounding Box)를 3차원에 배치시키기위한 feature를 얻기 위해 Depth Estimation이 필요하기도 하는데 Depth Estimation에서는 Edge 부분의 모호함 때문에 long tail이 발생하기도 합니다. 따라서 경계부분에 대한 정확도를 높이기 위해 Pseudo Lidar와 instance segmentation를 활용하자는 논문입니다.
이후에는 Pseudo Lidar까지는 필요 없고, 중앙 좌표기준으로 크기를 예측하는 CenterNet 혹은 uncertainty 등을 활용하는 방법도 제안이 되었습니다.
https://arxiv.org/pdf/1903.09847.pdf
c. Stereo Vision
Stereo Vision은 두 개의 이미지를 이용해서 양안시차 이용하는 방식으로, 우리가 두 눈으로 깊이를 파악할 수 있듯이, 다음의 순서를 통해 depth 를 알아낼 수 있습니다.
이것을 구현하는 방식에는 직접적으로 Stereo Camera를 활용하는 방식이 있고, 2개 이상의 카메라를 통해 Multi-View Stereo(MVS)를 하는 방식이 있습니다.
아래는 Stereo Vision에 필요한 간단한 과정에 대해서만 보여드리려고 합니다. (정말 간단)
- 1. Matching : 여러가지 사진의 world 좌표계 상에서의 동일한 점을 찾는 과정입니다. 아래 첫번째 그림은 Multi-View Stereo 방식에서 sparse하게 point-to-point로 matching한 결과이고, 두번째 그림은 Stereo 카메라를 활용해 얻은 두개의 이미지 간의 matching을 한 결과입니다. 역시나 stereo 카메라로 얻은 두 이미지 간의 matching은 앞서의 방식보다 는 dense한 matching 입니다.
또한 아래 그림과 같은 방식 말고도, epipolar geometry를 활용한 다른 방식도 있습니다.


- 2. Rectification : 매칭 시에 일치하지 않는 점 사이를 없애서 일치하도록 같은 plane에 평행하게 위치시키는 방법입니다. 앞서 b. Intrinsic Parameter를 활용한 변환에서 설명한 바와 같이 이 plane을 epipolar plane이라고 하며, recified 된 두 이미지의 epipolar line은 평행하게 위치하며 같은 평면 위에 위치하게 됩니다.
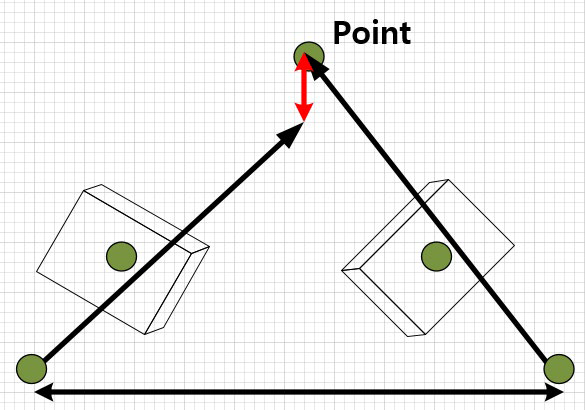
- 3. Triangulation : Distance를 구하는 방법입니다. 왼쪽 이미지와 오른쪽 이미지의 correspondence를 통해 3d point 값을 얻을 수 있습니다.
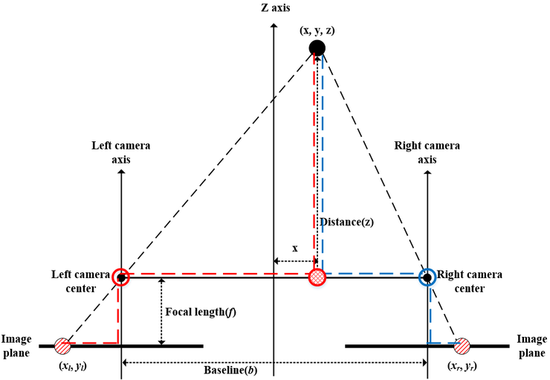
참고로 colmap이라는 오픈소스 툴을 통해 사진을 가지고 3D 데이터를 만들어내 볼 수도 있는데, 여기서도 MVS를 활용했습니다. (+ 뒤에서 설명할 SFM)
d. Ego의 Motion을 활용한 방법
물체의 주위를 여러 위치에서 촬영할 때 발생하는 카메라(혹은 Ego)의 움직임을 유추하고, 이를 바탕으로 3차원 형상 혹은 Ego의 Pose를 복원하는 방법에는 SFM(Structure From Motion), SLAM(Simultaneous Localization and Mapping), Visual Odometry가 있습니다. (SFM, SLAM은 3차원 형상 복원이 주목적, Visual Odometry는 Ego의 Pose 추정이 주목적)
자세한 내용보다는 개념에 대한 소개를 위주로 하려고 합니다.
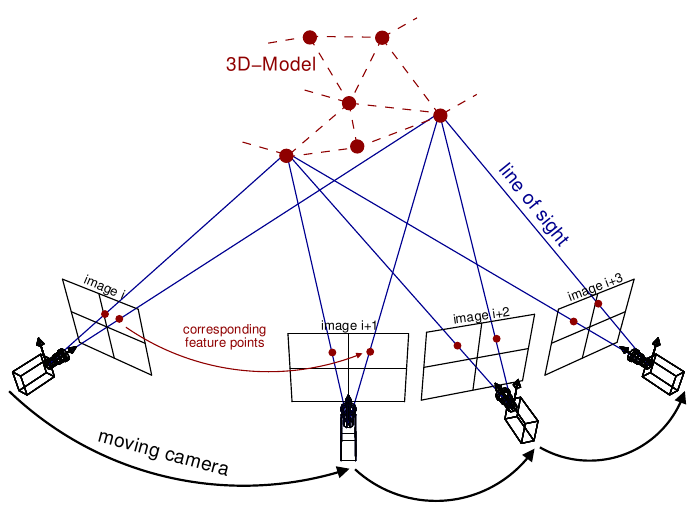
먼저, SFM은 말 그대로 주변 물체의 구조나 정보를 통해 모션을 측정해서 형태를 복원하는 과정입니다. 아래 그림은 SFM의 예시입니다.
SLAM은 SFM 혹은 다른 방법을 활용해 달성할 수 있습니다. 현재 visual camera의 위치를 추정하는 문제로, 자율주행 차량에 사용되어 주변 환경 지도를 작성하는 동시에 차량의 위치를 작성된 지도 안에서 추정하는 방법입니다. GPS등을 활용해 위치를 추정하는 Localization과 Map을 구축하는 Mapping의 혼합된 개념이라고 생각하시면 될 것 같습니다. 주로 static object 들이 타겟입니다.
Visual Odometry란 연속된 이미지를 활용해 실시간으로 카메라의 움직임을 estimation 하는 방법입니다. 센서의 종류에는 모터에 달린 Encoder 센서와 IMU(Inertial Measurement Unit, 관성측정장비)가 있는데, 차량에 부착된 센서는 바퀴 회전수를 주로 측정하지만, 로봇에서 사용되는 센서는 지나온 거리(distance) 뿐만 아니라 전체적인 로봇의 궤적(trajectory)을 포함한다고 합니다. 이를 활용해 모든 시간 t에 대해 6-DOF 궤적을 구축해 예측합니다.
** 6-Depth of Field(DOF) : X,Y,Z,Yaw,Pitch,Roll
참고로, Nuscenes와 Waymo 데이터셋에서는 key frame 과 주변 영상(sweep)의 속도 정보 혹은 GPS정보를 활용해 Motion Compensation으로 연속 3D정보를 매칭하기도 합니다. 즉, 연속된 3D정보를 얻어내고 나면 위 정보등을 활용해 연속된 데이터를 매칭할 수 있다는 뜻입니다.
e. Scene Flow & Optical Flow
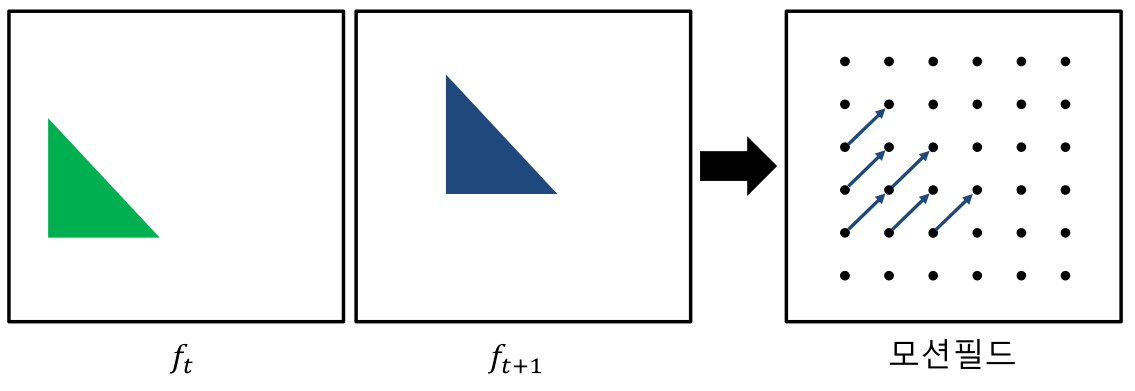
관찰자와 타겟 사이의 상대적인 움직임으로 인한 겉보기 움직임을 통해 이미지 상에서의 움직임을 활용하는 방법입니다. Scene Flow와 Optical Flow가 있는데, Optical Flow는 이미지 2D plane상에서의 인접한 frame간의 pixel motion field를 알아내는 과정이고, Scene Flow는 인접한 frame 간의 world 좌표계 3차원 상에서의 3D motion field를 알아내는 과정입니다. Scene Flow의 경우 scene structure를 복원하기 위해 stereo-based의 depth를 활용하는 경우도 있지만, 최근엔 RGB-D image 혹은 직접적으로 라이다 등의 Point Cloud를 활용하는 경우도 있습니다.
결과적으로, 둘 다 '장면'에서 일어나는 움직임을 기술하는 방법으로, 주로 Moving Object를 타겟팅합니다. 위 내용은 아래 논문에 개념에 대해 자세히 설명되어 있으며, 아래 그림은 Optical Flow의 Motion Field에 대한 예시 그림입니다.
https://arxiv.org/pdf/2203.15089.pdf
https://www.mathworks.com/help/vision/ug/fisheye-calibration-basics.html
https://edward0im.github.io/engineering/2019/11/12/euler-angle/
https://nghiaho.com/?page_id=846
https://foss4g.tistory.com/1665
https://www.cs.cmu.edu/~16385/s17/Slides/13.1_Stereo_Rectification.pdf
https://luckygg.tistory.com/35
'Developers 공간 [Basic] > Vision & Audio' 카테고리의 다른 글
| [Generative] Stable Diffusion 그 이후 (0) | 2024.06.06 |
|---|---|
| [NLP] GPT 기초 정리 (1) | 2024.06.06 |
| [Dataset] Waymo Open Dataset 개요 (0) | 2022.12.21 |

