[Pytorch] Attention Layer 분석 및 구축하기

2023. 6. 20. 16:02ㆍDevelopers 공간 [Basic]/Software Basic

728x90
반응형

이번엔 다양한 논문 및 네트워크 아키텍처에서 자주 활용되는 Attention Layer를 구축한 사례에 대해서 정리해보고자합니다.

 

물론 내가 만드는 네트워크의 'task에 따라서', '원하는 input feature의 modal'에 따라서 다양하게 사용할 수 있겠지만, 보통 어떻게 활용되는지 혹은 왜 쓰는지에 대해 파악하고 나면 사용하기 쉬울 것이라는 생각이 듭니다.

 

해당 코드는 Transformer, DeTR, 3DeTR 세가지 모델을 참조했으며, 각각 코드는 아래에서 참조했습니다.

Transformer : https://github.com/hyunwoongko/transformer

DeTR : https://github.com/facebookresearch/detr

3DeTR : https://github.com/facebookresearch/3detr

 

<구성>
1. Attention Layer
    a. Class Definition
    b. Layer Forward Call
2. Transformer Layer
    a. Transformer Layer
    b. Encoder Layer
    c. Decoder Layer
3. Encoder-Decoder Example

글효과 분류1 : 코드

글효과 분류2 : 폴더/파일

글효과 분류3 : 용어설명

글효과 분류4 : 글 내 참조

1. Attention Layer

먼저, 아래와 같이 pytorch 레이어 중 MultiheadAttention가 무엇인지, 어떤 의미를 가지는지 살펴보려고 합니다. 

 

[출처 : Attention is All You Need]

기존 Multi-Head Attention은 Attention is All You Need(https://arxiv.org/abs/1706.03762)라는 논문에서 소개되었으며, 그림은 위와 같습니다. 위 그림의 왼쪽에 있는 Scale Dot Product Attention하나를 약식으로 Attention이라고 부르는 경우도 있으며, 실제 수식은 아래와 같습니다. Attention 함수는 Additive Attention과 Dot-Product (Multiplicative) Attention으로 나뉘는데, 아래는 그 중 Dot-Product Attention과 유사하며, 더 빠르고 Space-efficient하다고 합니다.

** Additive Attention : MLP를 활용해 계산합니다

$$ Attention = Softmax(\frac{QK^{T}}{\sqrt{d_{k}}})*V $$

위 Q(Query), K(Key), V(Value)는 각각 벡터 형태를 가지고 있고 Key와 Value는 대부분 같은 데이터를 의미합니다. (뒤에서 어떤 부분이 다른지 언급하겠습니다.)

 

또한 위 수식중 아래와 같은 표현의 의미에 대해서 살펴보려고 합니다.

$$\frac{QK^{T}}{\sqrt{d_{k}}}$$

위 수식은 Scaled-Dot Product라고 불리며, Q와 K간의 Consine Similarity를 구한 것이라고 할 수 있습니다. 사실은 Dot Product 겠지만 Key와 Query와 얼마나 비슷한지를 나타내기 위한 방법으로 사용됐으므로 이렇게 표현했습니다. 사실 Dot Product와 Cosine Similarity의 차이는 결과 값이 각 벡터의 Magnitude로 scaled 되었는 지의 차이입니다. 자세한 내용에 대해서는 아래 "더보기"를 눌러 파악하시기를 추천드립니다.

 

d_k는 key와 query의 dimension을 의미하며, d_k가 작을 때는 Additive Attention과 Dot Product Attention이 비슷하게 동작합니다. 하지만 d_k가 클때는 additive attention이 dot product 보다 더 잘 동작한다고 합니다. 이는 d_k가 클수록 dot product값이 굉장히 커지기 때문에, 그 다음에 오는 SoftMax 레이어의 gradient값이 굉장히 작아지기 때문입니다. 따라서 이 효과를 없애기 위해 d_k로 scale을 해주었고, 이를 Scaled-Dot Product라고 부르게되었습니다.

 

그리고 이후에 V를 곱해주는 것은 위를 통해 얻은 "Value→Query Similarity"를 활용해, Key가 Query와 얼마나 비슷한지를 얻는 것이라 볼 수 있습니다.

 

더보기

-----------------------------------------------------------------------------------------------------

<Similaity Measurement Techniques>

Similarity distance measure이란 수학과 데이터 마이닝에서 자주 활용되는 개념으로, 두개의 object간의 얼마나 동질성을 가지고 있는지 측정하는 지표입니다. 대부분 적으면 적을수록 비슷하다는 것을 의미하겠지만, 아닌 경우도 있습니다. 아래 그림과 같이 다양한 Similarity Metric들이 존재하지만 Euclidean, Manhattan, Minkowski, Cosine, Pearson, Spearman, Mahalanobis, Jaccard 8가지를 설명하고자 합니다.

[https://towardsdatascience.com/17-types-of-similarity-and-dissimilarity-measures-used-in-data-science-3eb914d2681]
  • Euclidean Distance (L2 Norm)

가장 흔한 기법으로, 두 벡터간의 직선 거리를 측정하는 방법입니다.

$$UclideanDistance=\sqrt{\sum_{i}^{}(p_i-q_i)^2}$$

  • Manhattan Distance (L1 Norm)

역시 가장 흔한 기법으로, 두 점 사이의 거리를 각각의 절대값의 합으로 표현하는 방법입니다.

$$ManhattanDistance=\sum_{i}^{}|p_i-q_i|$$

  • Minkowski Distance

위 두가지 Euclidean과 Manhattan를 일반화한 거리입니다. 즉, 아래의 p가 1일 때 Manhattan, p가 2일 때 Euclidean이라 할 수 있습니다.

$$MinkowskiDistance=(\sum_{i}^{}|p_i-q_i|^p)^{\frac{1}{p}}$$

  • Cosine Similarity

코싸인 유사도는 두 벡터가 이루는 각도를 측정하는 방식입니다. 벡터의 크기와는 상관없이 두 벡터 간의 각도를 고려하므로 자주 쓰입니다. 1에 가까울 수록 비슷한 것을 의미하며, -1에 가까울 수록 각도 차이가 큰 것을 의미합니다. 또한 0인 경우에는 Orthogonal, 즉 수직(Perpendicular)인 것을 의미합니다.

$$CosineSimilarity = \frac{A\cdot B}{||A||||B||}$$

 

** Dot Product (Inner Product)

사실 Dot Product와 Cosine Similarity 간의 차이는 각 벡터의 Magnitude로 scaled되었는지의 차이입니다.(즉, vector1과 vector2의 크기와 두벡터간의 각도를 곱한 결과가 Dot Product입니다.) 따라서 (-∽~∽)의 값을 가지며 값이 클수록 비슷한 것을 의미합니다.

$$DotProduct = A\cdot B$$

Machine Learning에서 dot product를 두 벡터간의 similarity로 활용하는 경우가 많습니다. 하지만, 예를 들어, v1(2,2)와 v2(3,3)간의 dot product는 12인데, v1(2,2)와 v1(2,2)간의 dot product는 8입니다. 그럼 전자가 더 similar 하다는 걸까요? 그렇다고 보는 것입니다. 왜냐하면 이 것을 이해할때, magnitude와 direction을 모두 고려하기 때문에 magnitude의 값도 중요하다고 보는 것입니다.

 

  • (사전지식 설명) Covariance(공분산)

일반적으로 확률 변수 X에 대해 분산(Variance)은 아래와 같이 표현할 수 있습니다.

$$Var(X) = E[(X-E(X))^{2}]$$

이와 다르게, 두 확률 변수 X와 Y가 얼마나 함께 변하는지는 측정하기 위해서는 공분산(Covariance)를 즉정하며, 예를 들어 변수 X가 커질 때 다른 변수Y가 함께 커지는 것과 같이 변화의 방향이 같다면 Covariance는 양의 값을 가지게 됩니다. 또한 변수 X가 변해도 Y가 영향을 받지 않는다면 Covariance는 0이 됩니다. 수식은 아래와 같습니다.

$$CoVar(X,Y) = E[(X-E(X))(Y-E(Y))]=\sum_{i}^{}\frac{(X_i-\bar{X})(Y_i-\bar{Y})}{N-1}$$

예로, (1,2,3,4,5) 와 (2,3,4,5,6)의 covariance = (-2,-1,0,1,2)와 (-2,-1,0,1,2)의 곱의 평균 = (4,1,0,1,4)의 평균 = 2.5 입니다. 따라서 양수이므로 두 값의 증가방향이 같다고 볼 수 있습니다.

  • (사전지식 설명) Correlation

먼저, 헷갈릴 수도 있겠지만 Correlation Coefficient(상관계수)는 통계학에서 사용되는 용어이고, Cross Correlation과 Auto Correlation은 신호처리 분야의 용어입니다. 수식적으로는 비슷해보일 수 있으며, 목적이나 사용용도가 다릅니다. 예를 들어, Correlation Coefficient는 두 확률 변수 간의 연관관계만을 나타내는 것이며 , Cross Correlation은 음성신호와 영상신호의 실제 형태적 유사성을 수치적으로 계산한 것입니다.

즉, Correlation Analysis는 두 확률 변수 사이의 관련성을 파악하기 위한 방법이며, Correlation Coefficient는 두 변수간 관련성을 나타내기 위한 척도입니다. 이 글에서는 Correlation Coefficient를 다루겠습니다.

 

  • Pearson Correlation Coefficient

피어슨 상관 계수는 Covariance와 같이 두 확률 변수 간의 선형적 상관관계를 측정하지만 [-1~1] 사이 값을 가집니다. 즉 공분산을 각각 X와 Y의 표준편차로 나눠준 값입니다. 1이면 상관관계가 높다는 것을 의미하며, 0이면 상관관계가 없으며, -1이면 상관관계가 반대라는 것을 의미하며 수식은 아래와 같습니다.
$$\rho (X,Y) = \frac{CoVar(X,Y)}{\sigma_{x}\sigma_{x}}$$

  • Spearman's Rank Correlation Coefficient

스피어만 상관계수는 피어슨 상관 계수와 마찬가지로 [-1~1] 값을 가지지만, 연속형 데이터에 적합한 피어슨 상관계수와 달리 이산형 데이터와 순위형 데이터에 적용이 가능하다는 특징을 가지고 있습니다. 1이면 상관관계가 높다는 것을 의미하며, 0이면 상관관계가 없으며, -1이면 상관관계가 반대라는 것을 의미하며 수식은 아래와 같습니다.

$$\rho=\frac{\sum_{i}^{}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i}^{}(x_i-\bar{x})^2}\sqrt{\sum_{i}^{}(y_i-\bar{y})^2}}$$

 

** 자료형 구분

Categorical Data (범주형)
- Qualitative (질적)		 Ordinal Data (순위형) ex) 1,2,3 학년
Nominal Data (명목형) ex) 남, 녀
Numerical Data (수치형) 
- Quantitative (양적)		 Discrete Data (이산형) ex) 교통사건 건수
Continuous Data(연속형) Interval (간격) ex) 온도
Ratio (비율) ex) 키, 체중
  • Mahalanobis Distance

Multivariate Statstical Testing에 주로 사용되는 기법입니다. 예를 들어 아래 그림과 같이 두개의 feature가 있을 때, 두가지의 feature를 가진 데이터가 각각의 feature의 mean으로 부터의 Euclidean distance가 같은 값을 가지며 존재하더라도, 실제 두가지의 feature를 모두 고려한 데이터의 분포를 고려하면 그 similarity는 다를 수 있습니다. 
** Multivariate : 독립변수가 여러개인 경우

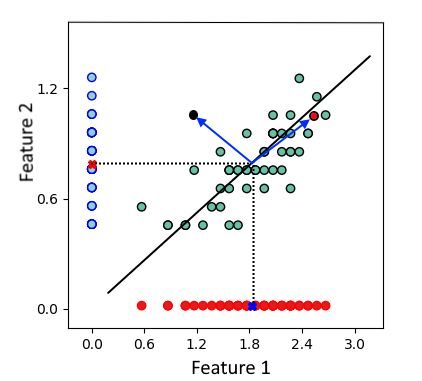
[https://towardsdatascience.com/17-types-of-similarity-and-dissimilarity-measures-used-in-data-science-3eb914d2681]

수식은 아래와 같으며, 두개의 feature간의 covariance를 고려한다는 것이 특징입니다. 

$$MahalanobisDistance=\sqrt{(P-Q)^T\cdot C^-1\cdot (P-Q)}$$

여기서 C(Covariance) matrix는 아래와 같이 표현할 수 있습니다.

$$ CoVar(P,Q)=\begin{pmatrix}
S_{P}^2 & S_{pq} \\
S_{qp} & S_{Q}^2 \\
\end{pmatrix}$$

  • Jaccard Distance

두 개의 dataset, 즉 "Set" 간의 유사도를 측정할 때 주로 사용되는 metric으로, 1이면 같은 데이터 0이면 다른 데이터라고 할 수 있습니다. Semantic Segmentation, Text Mining, E-Commerce, Recommendation System에서 자주 사용되며, intersection을 union으로 나누는 방법을 활용하기 때문에, 실제로 상대적인 Set의 비율을 활용한다고 볼 수 있습니다. 수식은 아래와 같습니다.

$$JaccardDistance=\frac{|P\cap Q|}{|P\cup Q|}$$

Text Mining 에서 Consine Similarity와 Jaccard Distance가 많이 사용되는데, Cosine Similarity는 "방향성"을 구하는데 집중한다고 하면, Jaccard Distance는 "동일한 것들의 비율"을 구하는 집중하는 것처럼 보입니다.

-----------------------------------------------------------------------------------------------------

 

다시 아래 식에 대해서 살펴보면서 의미를 살펴보겠습니다.

$$ Attention = Softmax(\frac{QK^{T}}{\sqrt{d_{k}}})*V $$

위 식의 예시로 Query, Key, Value의 Sequence Length가 9이고, Embedding Dimension이 64로 동일할 때, 차원을 넣어 살펴보면 보면 아래와 같습니다.

[https://wikidocs.net/162098]

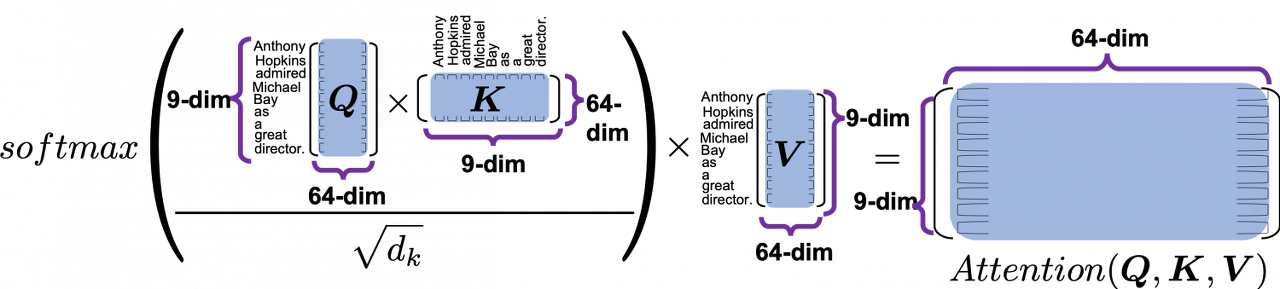
이중에 먼저 Query와 Key를 곱한 모습을 살펴보면 아래와 같습니다.

[https://wikidocs.net/162098]

이렇게 얻은 Attention Heat Map Matrix는 9x9 차원을 가질 것이며, 각 column이 어떤 의미를 가질지 살펴보면 "각 key의 모든 query 대한 weight를 어느정도로 가지고 있는지"를 나타내는 히트맵이라고 할 수 있습니다.(row는 반대로 "각 query의 모든 key 대한 weight를 어느정도로 가지고 있는지"를 나타내는 히트맵이겠죠)

또한 이렇게 얻은 Attention Heatmap은 sequence의 차원인 것을 보아, 이 heat map은 query와 key의 각각 sequence 별 "embedding의 consine similarity"를 의미한다고 볼수있습니다. 즉 위 예시에서는, query의 sequence차원(Anthony, Hopkins...)과 key의 sequence차원(Anthony, Hopkins...)에 대해 각각의 embedding 간 consine similarity를 알아낸 것입니다. 참고로 차원을 살펴보면, Key, Query의 Embedding Dimension은 같을 필요가 있지만, 이들이 Value의 Embedding Dimension과는 같을 필요가 없음도 알 수 있습니다. (Sequence간의 관계로만 나타내므로)

 

이번엔 Value를 곱했을 때의 의미를 살펴볼텐데, 의미를 조금 더 잘 보기 위해 transpose버전으로 살펴보면 아래와 같습니다. 

(transpose버전에서는 위와 반대로 각 column이 "각 query의 모든 key 대한 weight를 어느정도로 가지고 있는지"를 나타내는 히트맵일 것입니다)

[https://wikidocs.net/162098]
[https://wikidocs.net/162098]

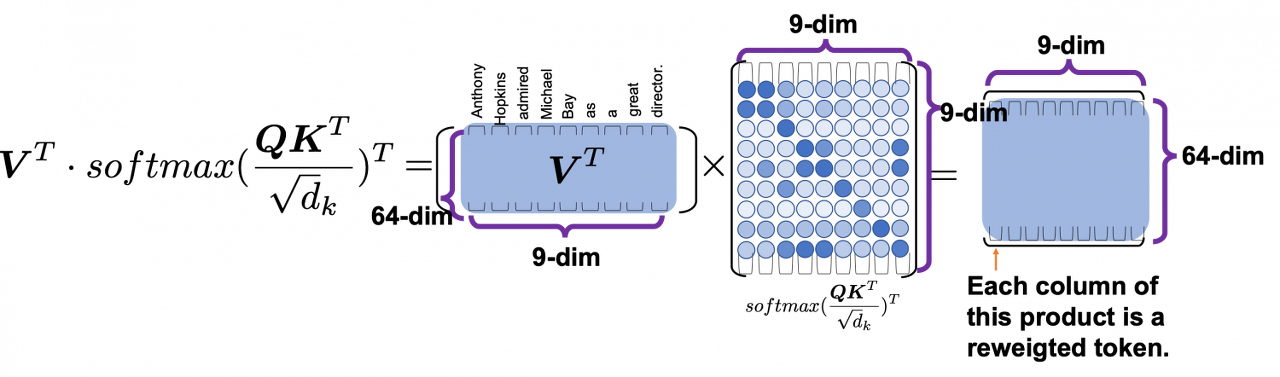
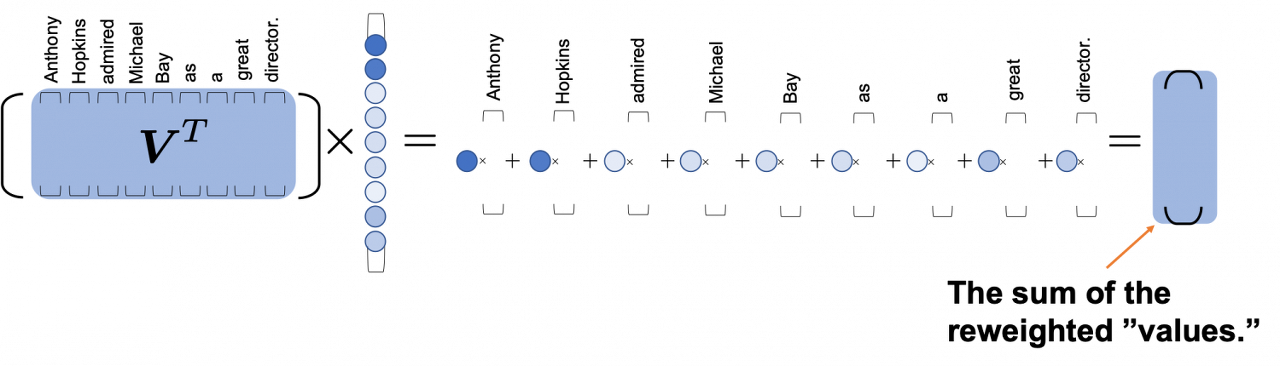
최종 결과는 64x9 차원을 가질 것이며, 이는 위 그림과 같이 "각 query(각 sequence)들의 value와의 비슷한 정도"의 "합"을 구하는 과정이라고 볼 수 있겠습니다.

 

또한 Key와 Value는 필수적으로 관계있는 값이어야겠지만, 항상 같은 역할을 하지는 않습니다. 즉, Key는 Query와의 연관성을 위해 Attention Heatmap을 만드는데 사용되지만, Value는 실질적으로 사용할 때 Key 내에서도 차등을 주어 Query와의 연관성을 얻어내야할 필요가 있다는 것이죠.

예를 들어, Query가 "network"가 들어왔고, Key는 "social"가 "sourcing"을 넣었다고 했을 때, "social network"와 "network sourcing" 모두 가능하고 Query와 Key간에는 두 관계가 비슷한 연관성을 가질 확률이 높습니다. 이 때 Value를 넣어줄 때 positional encoding을 해서 넣어준다면 결과적으로 다른 결과를 얻어낼 수도 있겠죠. 

 

 

[출처 : Attention is All You Need]

이번엔 위 그림 오른쪽에 보이는 것과 같이 Scaled Dot Product Attention 여러개를 활용해 Multihead를 구성하는데 이것은 무엇일까요?

원래 Attention Layer은 Input인 Q,K,V에 대해 dimension인 d_model을 동일하게 가지도록 합니다. 하지만 이들 Q,K.V를 각각 d_q(d_k와 값이 같겠죠?), d_k, d_v로 "head 개수인 h개"만큼 linear projection한 후에 attention을 병렬적으로 실행하는 것이 더 효율적이라는 것을 발견했습니다. 각각 head의 개수만큼 parallel하게 동작함으로써 다양한 representation을 다양한 위치에서 참조할 수 있도록 도와주는 것입니다. 함수와 차원은 아래와 같습니다.

$$MultiHead(Q,K,V) = Concat(head_{1},..., head_{h})W^{O}$$

$$\begin{matrix}
head_{i}=Attention(QW_{i}^{Q},KW_{i}^{K},VW_{i}^{V}) \\
Q,K,V\in R^{d_{model}} \\
W_{i}^{Q}\in R^{d_{model}\times d_{k}},W_{i}^{K}\in R^{d_{model}\times d_{k}}, W_{i}^{V}\in R^{d_{model}\times d_{v}}, W^{O}\in R^{hd_v\times d_{model}} \\
\end{matrix}$$

 

참고로, 아래서 살펴볼 pytorch의 MultiheadAttention을 활용하면 "AssertionError: embed_dim must be divisible by num_heads"에러를 보신적이 있으실 겁니다. 보통 이 layer를 사용할 때, d_k와 d_v를 직접줄 수도 있지만, 보통 head의 개수를 주고 전체 embedding dimension(d_model)이 나눠지도록 사용하게되는데, 정확하게 head의 개수로 주는 num_heads로 나눠떨어지지 않을 때 나는 에러입니다. 사실 나눠질 필요는 없지만, 보통 모든 head들이 같은 shape를 가지기를 원하므로 이런 에러를 주는 것 같습니다.

 

참고로, Transformer(Attention Is All You Need NIPS'17)는 input의 embedding dimension을 64로, head의 개수는 8로 주고 d_k와 d_v는 64/8인 8을 주어, 기존의 multihead를 적용하기 전과 후의 computational cost를 비슷하게 맞춰주었습니다.

 

마지막으로 Query, Key, Value로 들어오는 Input Embedding들의 sequence의 위치를 알기 위한 positional embedding(PE) 정보를 포함시키는 경우가 있습니다. Transformer는 Permutation Invariant한 특성을 가지기 때문에 Positional Embedding을 사용하게 되며, 종류에는 Funtion-based PE, Learned PE가 있습니다. 이중 Function-based는 MemN2N(End-To-End Memory Networks, NIPS'15)에서 사용한 것처럼 전체 length에 따라 결과를 다르게 주기 위한 함수를 사용하는 경우도 있고, Transformer(Attention Is All You Need NIPS'17)에서 사용한 Sinusoidal PE도 있습니다. 또한 Learned PE의 예로는 Bert(Pre-training of Deep Bidirectional Transformers for Language Understanding naacl'19)가 있습니다. 

** Permutation Equivariance : input의 순서가 바뀌는대로 output의 순서도 바뀌는 함수의 특성입니다. 예를 들어, (1,2,3)가 (a,b,c)출력을 낼 때, (1,3,2)는 (a,c,b) 출력을 냅니다. 

** Permutation Invariance : input의 순서가 바뀌어도 output의 순서는 바뀌지 않는 함수의 특성입니다. 예를 들어, (1,2,3)가 (a,b,c)출력을 낼 때, (1,3,2)는 (a,b,c) 출력을 냅니다. 

 

가장 많이 쓰이는 Sinusoidal PE의 식은 아래와 같습니다.

$$\begin{matrix}
PE_{pos,2i}=sin(\frac{pos}{10000^{\frac{2i}{d_{model}}}}) \\
PE_{pos,2i+1}=cos(\frac{pos}{10000^{\frac{2i}{d_{model}}}})
\end{matrix}$$

 

a. Class Definition

Multi-head Attention에 대해 자세히 알았으니, torch에 존재하는 MultiheadAttention 레이어에 대해서 먼저 살펴보고자합니다. 

[출처 : Attention is All You Need]

위 그림 중 오른쪽 그림과 같은 구성으로 되어있을 것은 예상하고 있으시겠지만, forward(query, key, value)를 했을 때 실제 어떤 순서로 동작하는 지를 나열해보면 아래와 같습니다. 이를 미리 설명드리는 이유는, 뒤에 함수에 대해서 설명할 때 어떤 step에 해당하는 절차인지를 명확하게 나타내기 위함입니다.

  1. input projection : 앞서 설명한 바와 같이 query와 key, value를 각각의 dimension으로 projection 시켜 줍니다.
    • 예를 들어, Key, Query의 차원이 (Seq_target, Batch, E_k), Value의 차원이 (Seq_source, Batch, E_v)인 경우, 결과적으로 Key, Query의 차원이 (Seq_target, Batch, E_k'), Value의 차원이 (Seq_source, Batch, E_v')이 됩니다.
      ** torch.nn.Linear(in_features, out_features, bias=True, device=None, dtype=None) : input과 output의 shape만 넣어줍니다.
      ** torch.nn.functional.linear(input, weight, bias=None) : input과 직접 weight와 bias를 넣어줍니다.
    • 미리 kdim과 vdim이 명시되지 않은 경우나 num_heads가 없는 경우 기존 차원을 유지합니다.
  2. (add_bias_kv) : key와 value의 bias를 넣어주기로 되어있다면, key와 value의 sequence length에 하나를 추가해줍니다.
    • 예를 들어, Key & Value의 차원이 (Seq_source, Batch, E_kv)인 경우, 결과적으로 bias를 (Seq_source+1, Batch, E_kv)로 바꿔줍니다.
  3. dimension change : query, key, value의 dimension을 (Batch*num_heads, Seq, head_dim)으로 변환 및 transpose해줍니다.
  4. (add_zero_attn) : attention에 zero dimension을 추가해주기로 되어있다면, key와 value에 dimension을 추가 해 줍니다.
    • 예를 들어, Key & Value의 차원이 (Batch*num_heads, Seq_source+1, head_dim)인 경우, 결과적으로 (Batch*num_heads, Seq_source+2, head_dim)가 됩니다.
  5. (key_padding_mask) : key의 mask가 있는 경우, mask를 만들어 줍니다.
  6. (attn_mask) : attention의 mask가 있는 경우, mask를 만들어 줍니다.
  7. attention : 위그림 왼쪽 Scaled Dot-product Attention과 같이 구성됩니다. 
    • [bmm > bias] > scaling  > (mask) > [softmax > dropout] > bmm 
      ** torch.bmm(input, mat2, *, out=None) : batch matrix-matrix product of matrices
    • 여기서 나오는 attn_output_weights의 경우 차원이 (Batch, num_heads, Seq_target, Seq_source)입니다.
  8. dimension change : attention output의 dimension을 (Seq_target, Batch, E_v'*num_heads)으로 변환해줍니다.
    • 사실 E_q는 E_k이며, 들어올 때와 같은 순서로 dimension을 맞춰줍니다.
  9. output projection : attention output을 각각의 dimension으로 projection 시켜 줍니다. (Seq_target, Batch, E_q)

 

위에서 Attention 알고리즘에 대해서 이해했으므로, 그것을 순서대로 구현했다고 생각하시고 가볍게 이해하시길 바랍니다. 이제 torch에 존재하는 MultiheadAttention 레이어를 선언하겠습니다.

torch.nn.MultiheadAttention(
            embed_dim, 
            num_heads, 
            dropout=0.0, 
            bias=True, 
            add_bias_kv=False, 
            add_zero_attn=False, 
            kdim=None, 
            vdim=None, 
            batch_first=False, 
            device=None, 
            dtype=None)
  • embed_dim : Attention Layer의 모델 dimension(d_model)을 넣어줍니다. 
  • num_heads :  병렬처리할 head의 개수를 의미합니다. (각각의 head는 embeded_dim//num_heads 의 차원을 가집니다.)
  • dropout : Attention Layer Output의 Dropout 확률을 의미합니다.
  • bias : 위 1번과 9번인 input/output projection에서 bias를 사용할 것인지를 명시합니다.
  • add_bias_kv : 위 2번인 bias_kv에서 input key와 value에서 bias를 추가해 줄 것인지를 명시합니다.
  • add_zero_attn : 위 4번인 add_zero_attn에서 zero attention을 추가해 줄 것인지를 명시합니다. 
  • kdim : 위 1번인 input projection에서 key의 dimension을 바꿔주는 경우 명시해줍니다.
  • vdim : 위 1번인 input projection에서 value의 dimension을 바꿔주는 경우 명시해줍니다. 
  • batch_first : False인 경우 (seq, batch, feature)이지만, True인 경우 (batch, seq, feature).

 

b. Layer Forward Call

이제 선언된 레이어를 활용해 forward() call을 부르는 경우를 살펴보겠습니다.

forward(
    query, 
    key, 
    value, 
    key_padding_mask=None, 
    need_weights=True, 
    attn_mask=None, 
    average_attn_weights=True)
  • query (Tensor) : Query 임베딩을 의미합니다.
    • unbatched : (Seq_target, E_q)
    • batch_first=False : (Seq_target, Batch, E_q)
    • batch_first=True : (Batch, Seq_target, E_q)
  • key (Tensor) : Key 임베딩을 의미합니다.
    • unbatched : (Seq_source , E_k)
    • batch_first=False : (Seq_source, Batch, E_k)
    • batch_first=True : (Batch, Seq_source, E_k) 
  • value (Tensor) : Value 임베딩을 의미합니다.
    • unbatched : (Seq_source, E_v) 
    • batch_first=False : (Seq_source, Batch, E_v) 
    • batch_first=True : (Batch, Seq_source, E_v) 
  • key_padding_mask (Optional[Tensor]) : 위 과정 중 5번의 key의 어떤 elements들을 masking할지 결정하는  mask입니다.
    • unbatched query : (Seq_source)
    • batch : (Batch, Seq_source)
    • 종류1. Binary masks : True가 해당 key value를 무시하겠다는 것을 의미합니다. 
    • 종류2. Byte masks(Float masks) : 해당 key에 더해집니다. 
  • need_weights (bool) : 위 과정 중 7번의 output인 attn_output_weights를 return 받을지 결정합니다.
  • attn_mask (Optional[Tensor]) : 위 과정 중 6번의 attention의 어떤 elements들을 masking 할지 2D 혹은 3D로 결정하는 mask입니다. 2D는 batch 전체에 적용되며, 3D는 batch 마다 다르게 적용할 때 쓰입니다. 
    • unbatched : (Seq_target, Seq_source)
    • batch : (Batch* #ofHeads, Seq_target, Seq_source)
    • 종류1. Binary masks : True가 해당 key value를 무시하겠다는 것을 의미합니다. 
    • 종류2. Byte masks : 해당 key에 더해집니다.
  • average_attn_weights (bool) : 하나의 head내에서 attn_weight를 평균값으로 얻어낼 지를 명시합니다.

2. Transformer Layer

 

그렇다면 위 함수를 활용해서 Attention Layer를 구성할 때, 보통 어떻게 구현했을까요? Attention Is All You Need(Transformer), DeTR, 그리고 3DeTR에서 이미지와 라이다 정보를 Feature Extraction하기 위해서 Layer를 어떻게 구현했는지에 대해서 살펴보려고합니다.

a. Transformer Layer 

먼저 Trasnformer에서 Encoder와 Decoder Layer를 구성한 기본 구조는 아래 그림과 같습니다. 아래와 같이 layer를 구성한 후에 encoder layer와 decoder layer를 각각 여러번 쌓아 Transformer구조를 만들어내는 것입니다.

 

Encoder와 Decoder의 같은 점은 feature extraction할 때 self-attention을 쓴다는 것이며, 다른 점은 Decoder는 multi-head attention도 활용한다는 점입니다. multi-head attention에서는 key, value를 "memory"라고 하는 encoder의 feature를 활용합니다.

feature extraction 할 때 key_padding_mask를 사용하는 것이나 positional embedding을 사용할지 등에 대해서는 어떤 feature인지에 따라 모두 다를 것입니다.

 

 

 

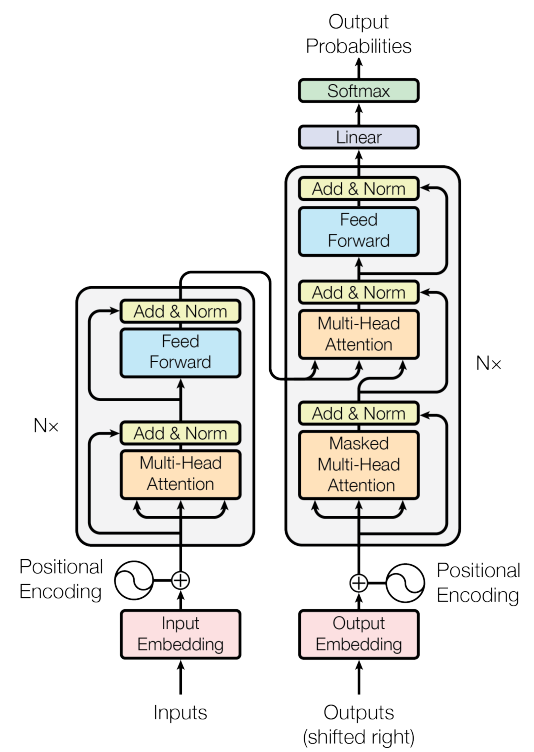
[Transformer의 Encoder와 Encoder Layer 구조]

 

위 Transformer의 Encoder Layer와 Decoder Layer를 구현한 내용은 아래와 같이 도식화해서 볼 수 있습니다. 보시다시피 위 그림과 동일하게 구현이 되어있는 것을 볼 수 있고, Feed Forward 레이어가 어떻게 생겼는지, Add&Norm 레이어가 어떻게 생겼는지 한눈에 볼 수 있습니다.

 

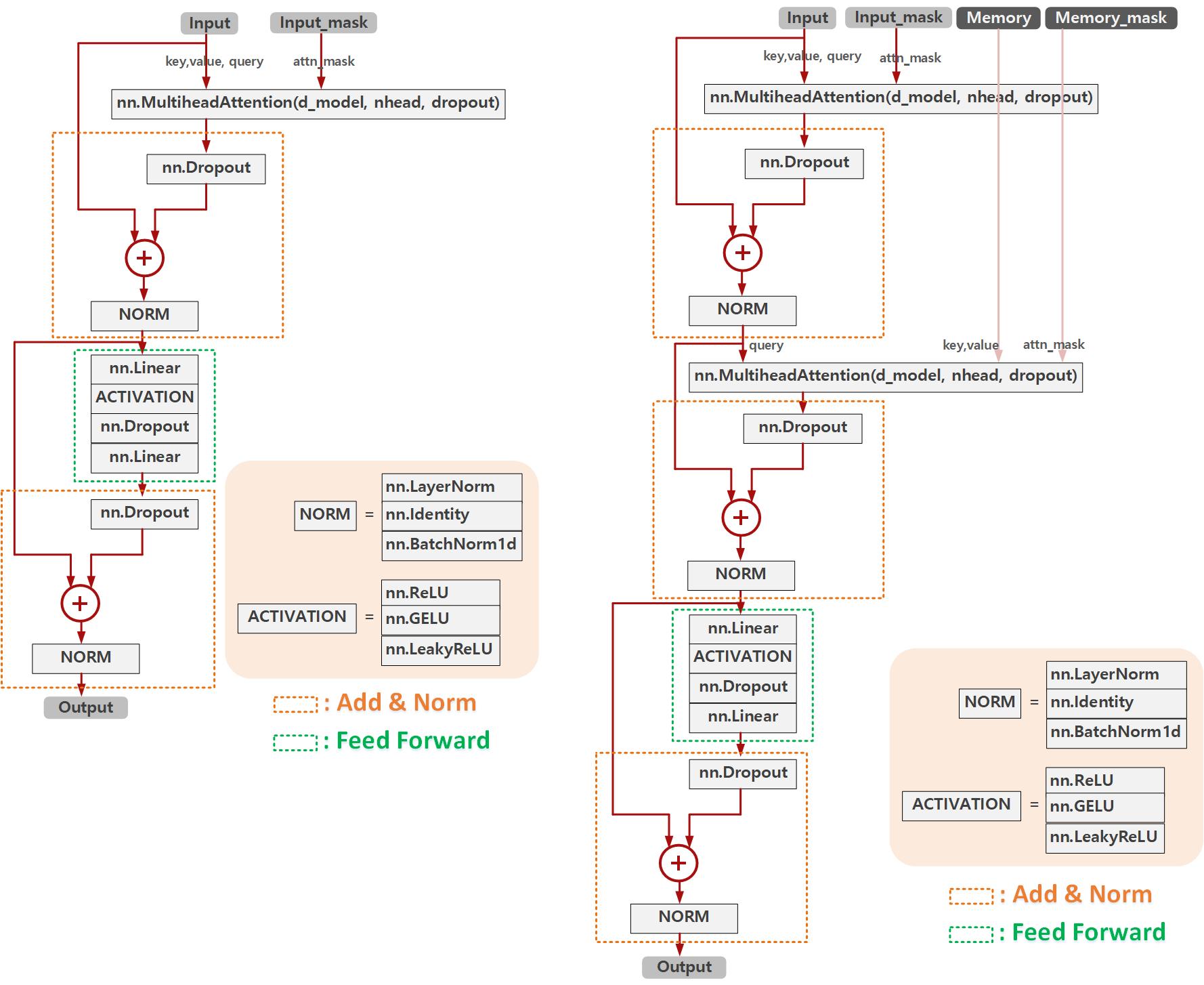
[Transformer의 Encoder Layer(왼쪽)과 Decoder Layer(오른쪽) 구조]

 

b. Encoder Layer

그렇다면 이번엔 DeTR과 3DeTR에서 Encoder Layer를 구성한 방법에 대해서 살펴보겠습니다. 아래 그림은 3DeTR과 DeTR에서 Encoder Layer를 구성한 모습을 도식화 해보였습니다. DeTR의 경우 위 도식과 동일하게 구현되어있고, 3DeTR의 경우 특이하게 Normalization을 생략했으며, Add&Norm 레이어의 대상을 이전 output 중 Normalization 이전의 값을 가져와 사용한 구조임을 알 수 있습니다.

 

 

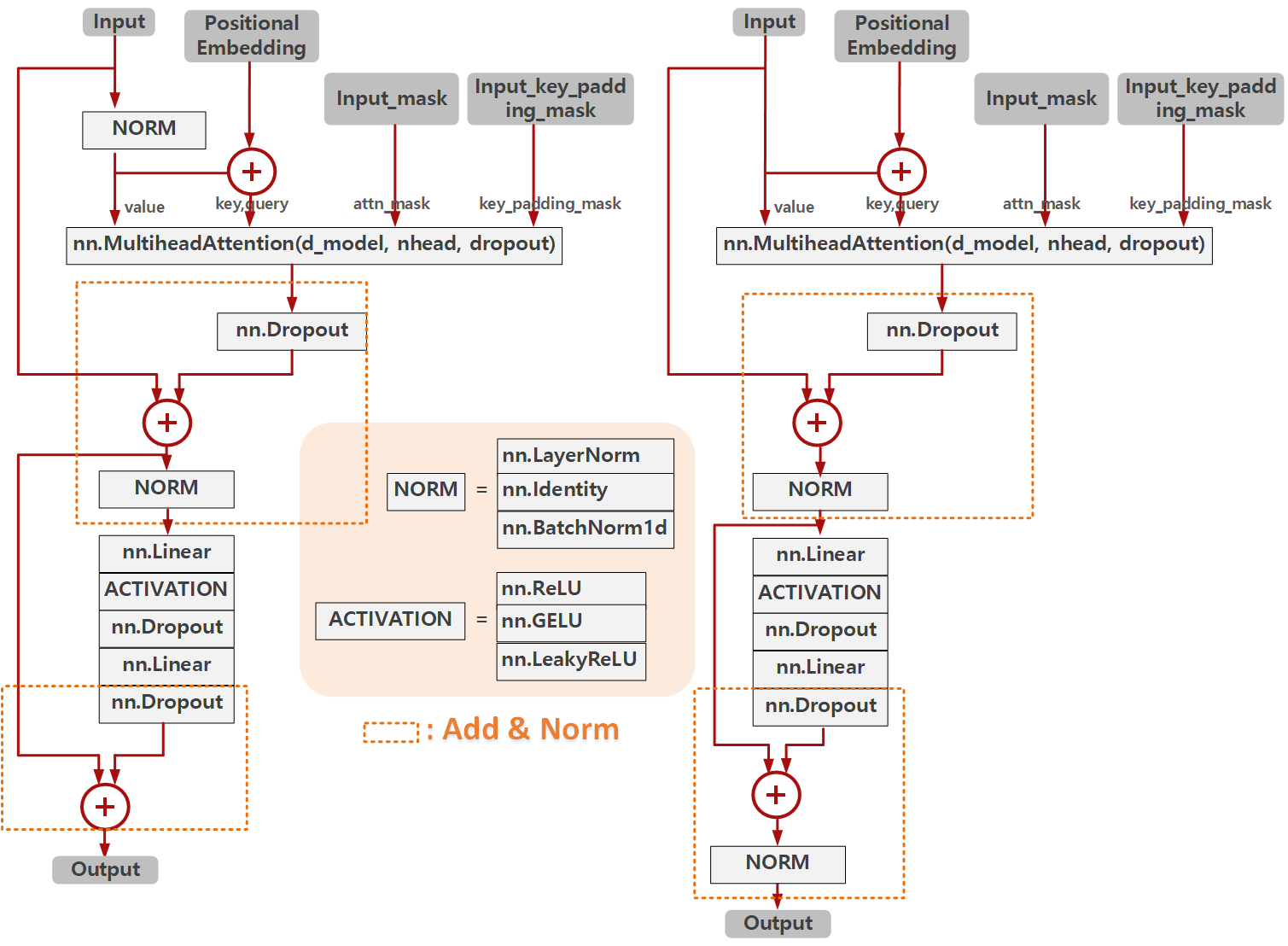
[3DeTR(왼쪽)과 DeTR(오른쪽)의 Encoder Layer 구조]

 

아래 코드는 위 구조 중 DeTR코드 중 Encoder Layer를 실제 구현한 모습을 보입니다.

from torch import Tensor, nn

class TransformerEncoderLayer(nn.Module):

    def __init__(self, 
                d_model, 
                nhead=4, 
                dim_feedforward=128,
                dropout=0.1, 
                dropout_attn=None,
                activation="relu", 
                normalize_before=True, 
                norm_name="ln",
                use_ffn=True,
                ffn_use_bias=True):
        super().__init__()
        if dropout_attn is None:
            dropout_attn = dropout
        self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout_attn)

        self.linear1 = nn.Linear(d_model, dim_feedforward, bias=ffn_use_bias)
        self.dropout = nn.Dropout(dropout, inplace=True)
        self.linear2 = nn.Linear(dim_feedforward, d_model, bias=ffn_use_bias)
        self.norm2 = NORM_DICT[norm_name](d_model)
        self.norm2 = NORM_DICT[norm_name](d_model)
        self.dropout2 = nn.Dropout(dropout, inplace=True)

        self.norm1 = NORM_DICT[norm_name](d_model)
        self.dropout1 = nn.Dropout(dropout, inplace=True)

        self.activation = ACTIVATION_DICT[activation]()
        self.nhead = nhead

    def with_pos_embed(self, tensor, pos: Optional[Tensor]):
        return tensor if pos is None else tensor + pos

    def forward(self, 
                src,
                src_mask: Optional[Tensor] = None,
                src_key_padding_mask: Optional[Tensor] = None,
                pos: Optional[Tensor] = None,
                return_attn_weights: Optional [Tensor] = False):
        q = k = self.with_pos_embed(src, pos)
        value = src
        src2, attn_weights = self.self_attn(q, k, value=value, attn_mask=src_mask,
                              key_padding_mask=src_key_padding_mask)[0]
        src = src + self.dropout1(src2)
        if self.use_norm_fn_on_input:
            src = self.norm1(src)
        if self.use_ffn:
            src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
            src = src + self.dropout2(src2)
            src = self.norm2(src)
        if return_attn_weights:
            return src, attn_weights
        return src

    def extra_repr(self):
        st = ""
        if hasattr(self.self_attn, "dropout"):
            st += f"attn_dr={self.self_attn.dropout}"
        return st

먼저, 위 코드를 활용해서 Transformer의 경우 아래와 같이 선언했습니다. 이렇게 하나하나 어떻게 선언했는지 남겨 놓는 이유는, d_model과 feed forward 레이어의 차원등을 한눈에 볼 수 있기 위함입니다.

forward() 과정에서 (src,  pos)를 사용했으며, (src_key_padding_mask, src_mask)는 사용하지 않았습니다.

encoder_layer = TransformerEncoderLayer(
    d_model=512,
    nhead=8,
    dim_feedforward=2048,
    dropout=0.1,
    activation="relu",
)

또한 DeTR의 경우 아래와 같이 선언했으며, forward() 과정에서 (src, src_key_padding_mask, pos)를 활용했으며 (src_mask)는 사용하지 않았습니다.

encoder_layer = TransformerEncoderLayer(
    d_model=256,
    nhead=8,
    dim_feedforward=2048,
    dropout=0.1,
    activation="relu",
)

또한 3DeTR의 경우 아래와 같이 선언했으며, forward() 과정에서 (src)만 사용했으며, (src_key_padding_mask, pos, src_mask)는 사용하지 않았습니다.

encoder_layer = TransformerEncoderLayer(
    d_model=256,
    nhead=4,
    dim_feedforward=128,
    dropout=0.1,
    activation="relu",
)
c. Decoder Layer

위와 같이 DeTR과 3DeTR에서 Decoder Layer를 구성한 방법에 대해서 살펴보겠습니다. 아래 그림은 3DeTR과 DeTR에서 Decoder Layer를 구성한 모습을 도식화 해보였습니다.

역시낭 위와 같이 DeTR의 경우 Transformer와 동일하게 구현되어있고, 3DeTR의 경우 특이하게 마지막 Normalization을 생략했으며, Add&Norm 레이어의 대상을 이전 output 중 Normalization 이전의 값을 가져와 사용한 구조임을 알 수 있습니다.

 

 

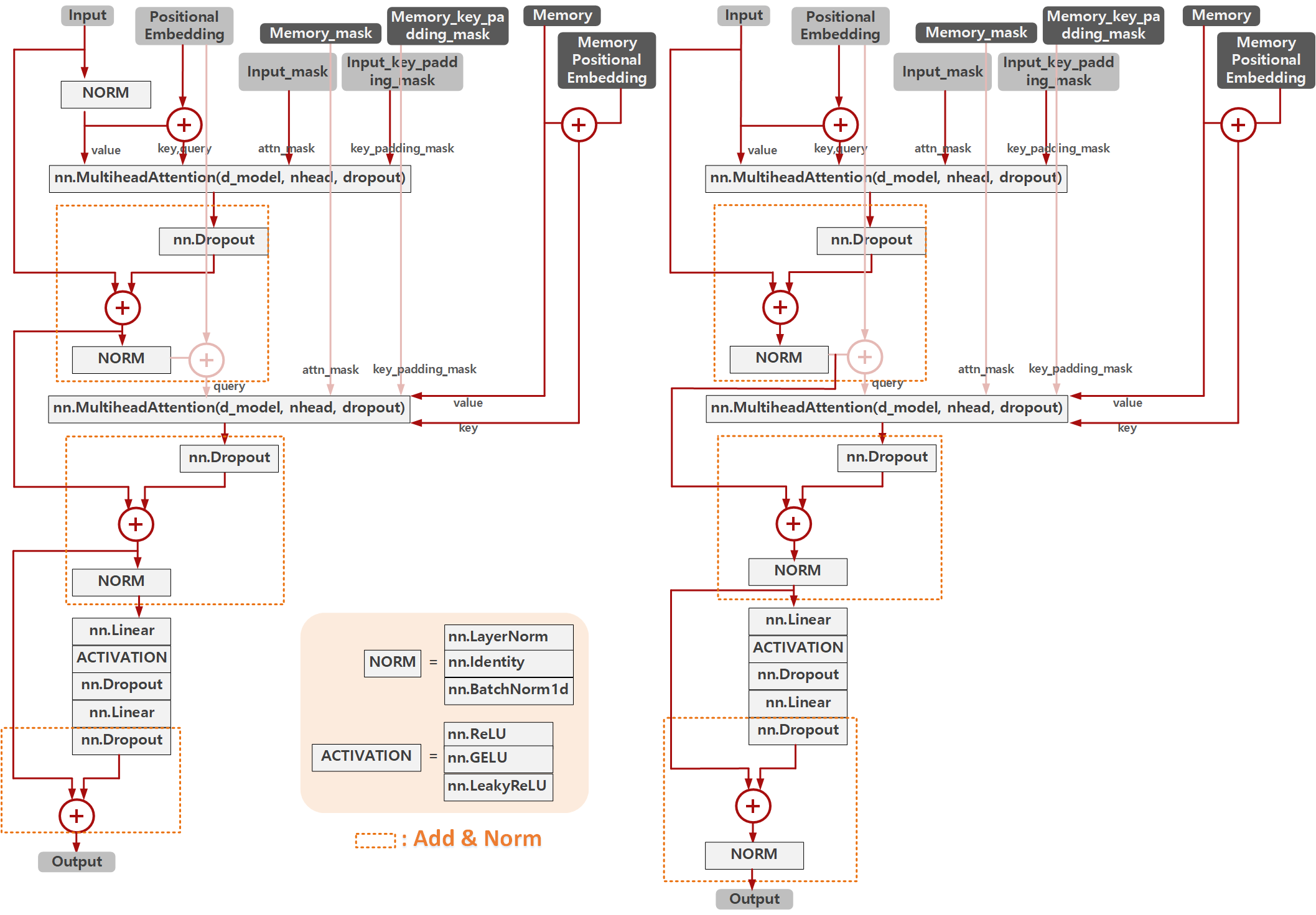
[3DeTR(왼쪽)과 DeTR(오른쪽)의 Decoder Layer 구조]

 

아래 코드는 위 구조 중 DeTR코드 중 Decoder Layer를 실제 구현한 모습을 보입니다.

from torch import Tensor, nn

class TransformerDecoderLayer(nn.Module):

    def __init__(self, 
                d_model, 
                nhead=4, 
                dim_feedforward=256,
                dropout=0.1, 
                dropout_attn=None,
                activation="relu", 
                normalize_before=True,
                norm_fn_name="ln"):
        super().__init__()
        if dropout_attn is None:
            dropout_attn = dropout
        self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
        self.multihead_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)

        self.norm1 = NORM_DICT[norm_fn_name](d_model)
        self.norm2 = NORM_DICT[norm_fn_name](d_model)

        self.norm3 = NORM_DICT[norm_fn_name](d_model)
        self.dropout1 = nn.Dropout(dropout, inplace=True)
        self.dropout2 = nn.Dropout(dropout, inplace=True)
        self.dropout3 = nn.Dropout(dropout, inplace=True)

        # Implementation of Feedforward model
        self.linear1 = nn.Linear(d_model, dim_feedforward)
        self.dropout = nn.Dropout(dropout, inplace=True)
        self.linear2 = nn.Linear(dim_feedforward, d_model)

        self.activation = ACTIVATION_DICT[activation]()
        self.normalize_before = normalize_before

    def with_pos_embed(self, tensor, pos: Optional[Tensor]):
        return tensor if pos is None else tensor + pos

    def forward(self, 
    			tgt, 
                memory,
                tgt_mask: Optional[Tensor] = None,
                memory_mask: Optional[Tensor] = None,
                tgt_key_padding_mask: Optional[Tensor] = None,
                memory_key_padding_mask: Optional[Tensor] = None,
                pos: Optional[Tensor] = None,
                query_pos: Optional[Tensor] = None,
                return_attn_weights: Optional [bool] = False):
        q = k = self.with_pos_embed(tgt, query_pos)
        tgt2 = self.self_attn(q, k, value=tgt, attn_mask=tgt_mask,
                              key_padding_mask=tgt_key_padding_mask)[0]
        tgt = tgt + self.dropout1(tgt2)
        tgt = self.norm1(tgt)
        tgt2, attn = self.multihead_attn(query=self.with_pos_embed(tgt, query_pos),
                                   key=self.with_pos_embed(memory, pos),
                                   value=memory, attn_mask=memory_mask,
                                   key_padding_mask=memory_key_padding_mask)
        tgt = tgt + self.dropout2(tgt2)
        tgt = self.norm2(tgt)
        tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
        tgt = tgt + self.dropout3(tgt2)
        tgt = self.norm3(tgt)
        if return_attn_weights:
            return tgt, attn
        return tgt, None

위 코드를 활용해서 Transformer의 경우 아래와 같이 선언했습니다. 

forward() 과정에서 target의 경우 (tgt,  tgt_mask, pos)를 사용했으며, (tgt_key_padding_mask)는 구현되어있지도 않습니다.  또한 memory의 경우 (memory, query_pos,  memory_mask)만 활용했으며, (memory_key_padding_mask)는 구현되어있지도 않습니다.

decoder_layer = TransformerDecoderLayer(
    d_model=512,
    nhead=8,
    dim_feedforward=2048,
    dropout=0.1,
)
#d_k, d_v = 64

또한 DeTR의 경우 아래와 같이 선언했으며, forward()과정에서 target의 경우 (tgt, pos)만 활용했으며, (tgt_mask, tgt_key_padding_mask)는 활용하지 않았습니다. 또한 memory의 경우 (memory, query_pos, memory_key_padding_mask)만 활용했으며, (memory_mask)는 활용하지 않았습니다.

decoder_layer = TransformerDecoderLayer(
    d_model=256,
    nhead=8,
    dim_feedforward=2048,
    dropout=0.1,
)

또한 3DeTR의 경우 아래와 같이 선언했으며, forward()과정에서 target의 경우 (tgt, pos)만 활용했으며, (tgt_mask, tgt_key_padding_mask)는 활용하지 않았습니다. 또한 memory의 경우 (memory, query_pos)만 사용했으며, (memory_mask, memory_key_padding_mask)는 활용하지 않았습니다.

decoder_layer = TransformerDecoderLayer(
    d_model=256,
    nhead=4,
    dim_feedforward=256,
    dropout=0.1,
)

 

3. Encoder-Decoder Example

위와 같이 Encoder Layer와 Decoder Layer를 활용해 실제 3가지 모델은 어떻게 모델을 구성했을 까요? 

사실 위 Layer까지 구현이 완료되면 Encoder와 Decoder를 구성하는 것은 Layer들을 활용해 아래와 같은 몇가지만 구현해주면 됩니다.

 

1. 기존의 구현한 Layer들을 정해진 개수만큼 반복해 구현합니다.

  Transformer DeTR 3DeTR
# of Encoder Layers 6 6 3
# of Decoder Layers 6 6 8

2. Image의 경우 Patchify하는 과정을 추가해 patch를 sequence dimension에 맞게 만들어주는 과정이 필요할 것입니다.

3. normalize가 필요한 경우 normalization layer를 추가해주어야 할 것입니다.

4. weight의 초기화를 해주어야 합니다.
** nn.init.xavier_uniform : weight initialization 기법으로 가장 흔하게 사용되는 방법입니다.

 

이를 활용해 Encoder의 구현 예시는 아래와 같습니다.

class TransformerEncoder(nn.Module):

    def __init__(self, encoder_layer, num_layers,
                 norm=None, weight_init_name="xavier_uniform"):
        super().__init__()
        self.layers = get_clones(encoder_layer, num_layers)
        self.num_layers = num_layers
        self.norm = norm
        self._reset_parameters(weight_init_name)

    def _reset_parameters(self, weight_init_name):
        func = WEIGHT_INIT_DICT[weight_init_name]
        for p in self.parameters():
            if p.dim() > 1:
                func(p)

    def forward(self, src,
                mask: Optional[Tensor] = None,
                src_key_padding_mask: Optional[Tensor] = None,
                pos: Optional[Tensor] = None,
                xyz: Optional [Tensor] = None,
                transpose_swap: Optional[bool] = False,
                ):
        if transpose_swap:
            bs, c, h, w = src.shape
            src = src.flatten(2).permute(2, 0, 1)
            if pos is not None:
                pos = pos.flatten(2).permute(2, 0, 1)
        output = src
        orig_mask = mask
        if orig_mask is not None and isinstance(orig_mask, list):
            assert len(orig_mask) == len(self.layers)
        elif orig_mask is not None:
            orig_mask = [mask for _ in range(len(self.layers))]

        for idx, layer in enumerate(self.layers):
            if orig_mask is not None:
                mask = orig_mask[idx]
                # mask must be tiled to num_heads of the transformer
                bsz, n, n = mask.shape
                nhead = layer.nhead
                mask = mask.unsqueeze(1)
                mask = mask.repeat(1, nhead, 1, 1)
                mask = mask.view(bsz * nhead, n, n)
            output = layer(output, src_mask=mask,
                           src_key_padding_mask=src_key_padding_mask, pos=pos)

        if self.norm is not None:
            output = self.norm(output)

        if transpose_swap:
            output = output.permute(1, 2, 0).view(bs, c, h, w).contiguous()

        xyz_inds = None

        return xyz, output,

선언 한 예시는 쉽기 때문에 3DeTR의 경우만 아래 처럼 보이겠습니다.

encoder = TransformerEncoder(
    encoder_layer=encoder_layer, 
    num_layers=3
)

 

다음으로 Decoder 의 구현 예시는 아래와 같습니다.

class TransformerDecoder(nn.Module):

    def __init__(self, decoder_layer, num_layers, norm_fn_name="ln",
                return_intermediate=False,
                weight_init_name="xavier_uniform"):
        super().__init__()
        self.layers = get_clones(decoder_layer, num_layers)
        self.num_layers = num_layers
        self.norm = None
        if norm_fn_name is not None:
            self.norm = NORM_DICT[norm_fn_name](self.layers[0].linear2.out_features)
        self.return_intermediate = return_intermediate
        self._reset_parameters(weight_init_name)

    def _reset_parameters(self, weight_init_name):
        func = WEIGHT_INIT_DICT[weight_init_name]
        for p in self.parameters():
            if p.dim() > 1:
                func(p)

    def forward(self, tgt, memory,
                tgt_mask: Optional[Tensor] = None,
                memory_mask: Optional[Tensor] = None,
                tgt_key_padding_mask: Optional[Tensor] = None,
                memory_key_padding_mask: Optional[Tensor] = None,
                pos: Optional[Tensor] = None,
                query_pos: Optional[Tensor] = None,
                transpose_swap: Optional [bool] = False,
                return_attn_weights: Optional [bool] = False,
                ):
        if transpose_swap:
            bs, c, h, w = memory.shape
            memory = memory.flatten(2).permute(2, 0, 1) # memory: bs, c, t -> t, b, c
            if pos is not None:
                pos = pos.flatten(2).permute(2, 0, 1)
        output = tgt

        intermediate = []
        attns = []

        for layer in self.layers:
            output, attn = layer(output, memory, tgt_mask=tgt_mask,
                           memory_mask=memory_mask,
                           tgt_key_padding_mask=tgt_key_padding_mask,
                           memory_key_padding_mask=memory_key_padding_mask,
                           pos=pos, query_pos=query_pos,
                           return_attn_weights=return_attn_weights)
            if self.return_intermediate:
                intermediate.append(self.norm(output))
            if return_attn_weights:
                attns.append(attn)

        if self.norm is not None:
            output = self.norm(output)
            if self.return_intermediate:
                intermediate.pop()
                intermediate.append(output)

        if return_attn_weights:
            attns = torch.stack(attns)

        if self.return_intermediate:
            return torch.stack(intermediate), attns

        return output, attns

선언 한 예시는 쉽기 때문에 3DeTR의 경우만 아래 처럼 보이겠습니다.

decoder = TransformerDecoder(
    decoder_layer, 
    num_layers=8, 
    return_intermediate=True
)

https://darkpgmr.tistory.com/185

https://pytorch.org/docs/stable/generated/torch.nn.MultiheadAttention.html

https://darkpgmr.tistory.com/185

https://towardsdatascience.com/17-types-of-similarity-and-dissimilarity-measures-used-in-data-science-3eb914d2681

https://github.com/pytorch/pytorch/issues/67999

 

 

 

728x90
반응형
저작자표시 비영리 변경금지

'Developers 공간 [Basic] > Software Basic' 카테고리의 다른 글

[PyTorch] Optimizer & LR Scheduler 정리  (0) 2024.08.17
[Python] Multi-process와 Multi-thread 구현하기  (0) 2024.01.21
[OOP] Design Pattern 정리  (0) 2023.05.15
[PyTorch] DDP(Distributed Data Parallel) 셋팅하기  (0) 2022.12.27
[AWS] SMDDP(Sagemaker's DDP) 기본 환경 셋팅  (0) 2022.12.27

관련글

댓글 0

티스토리툴바